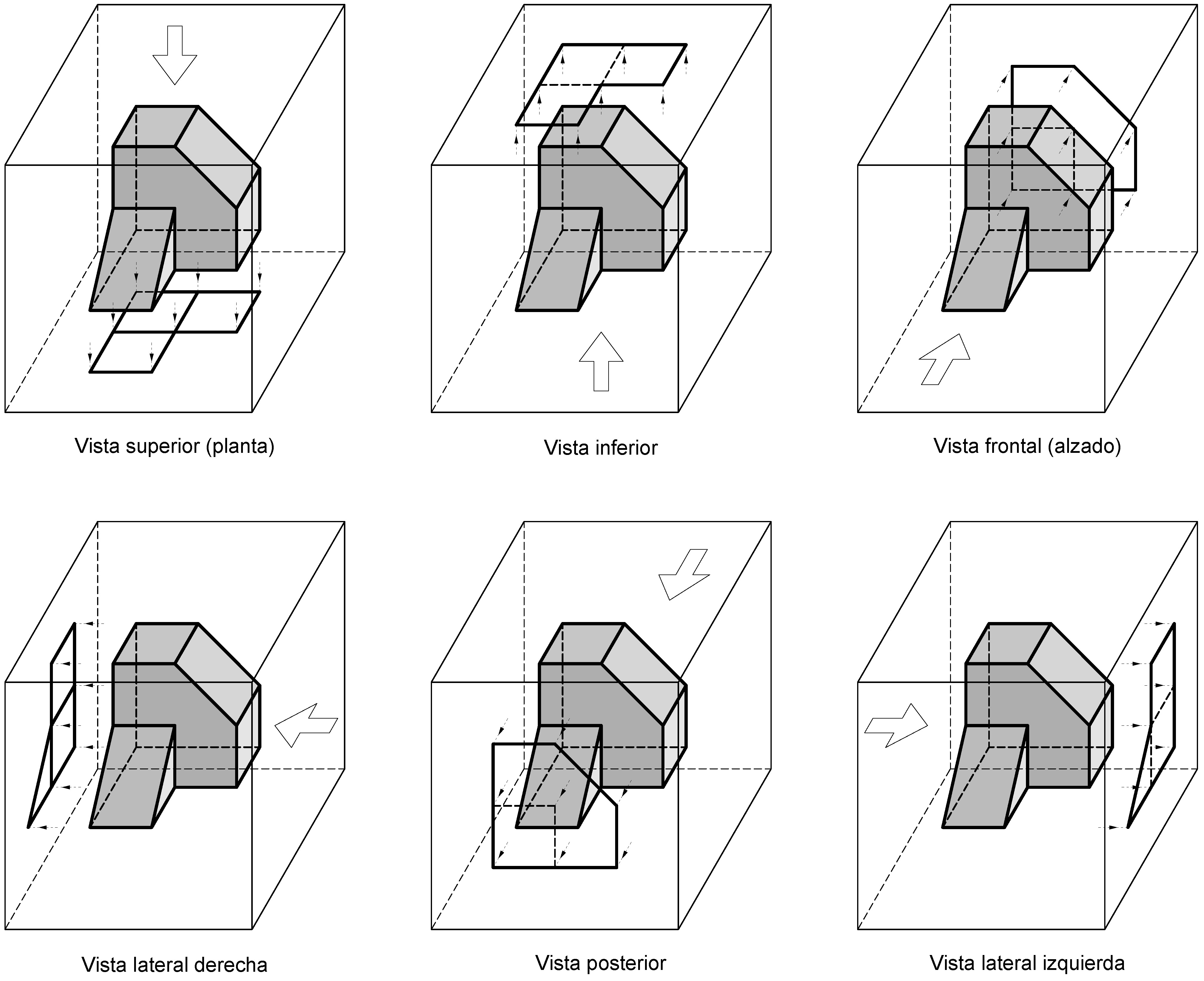
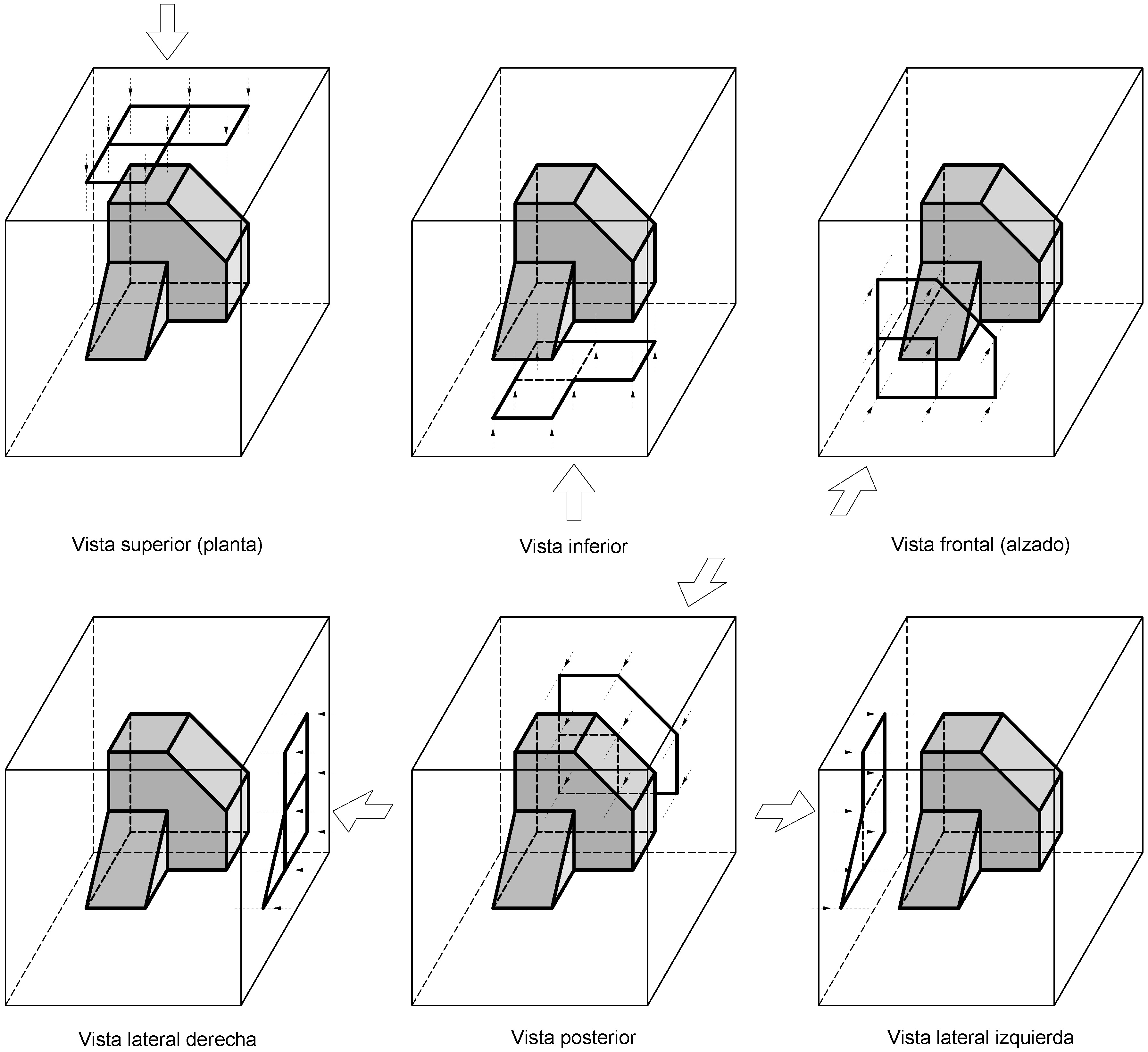
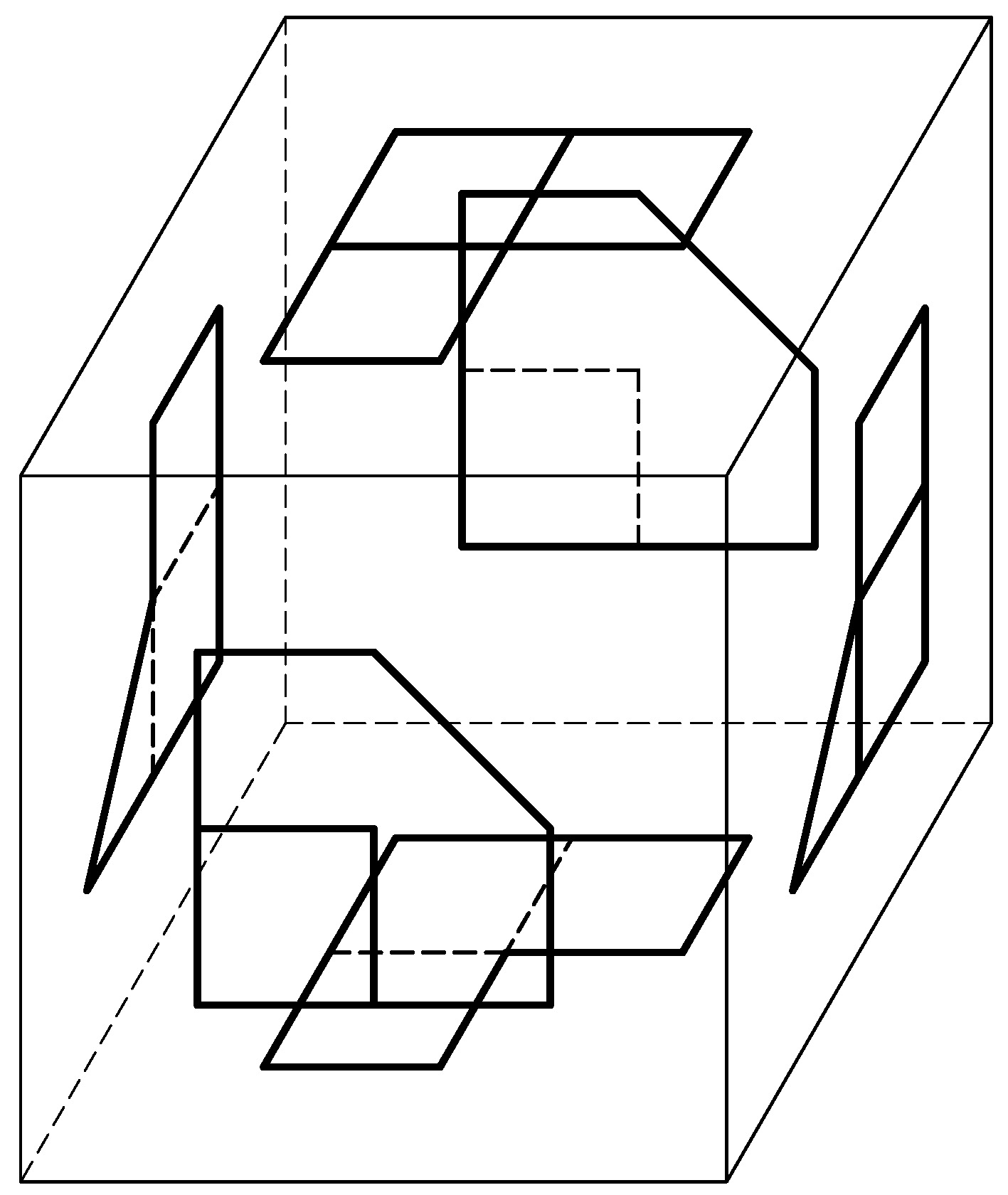
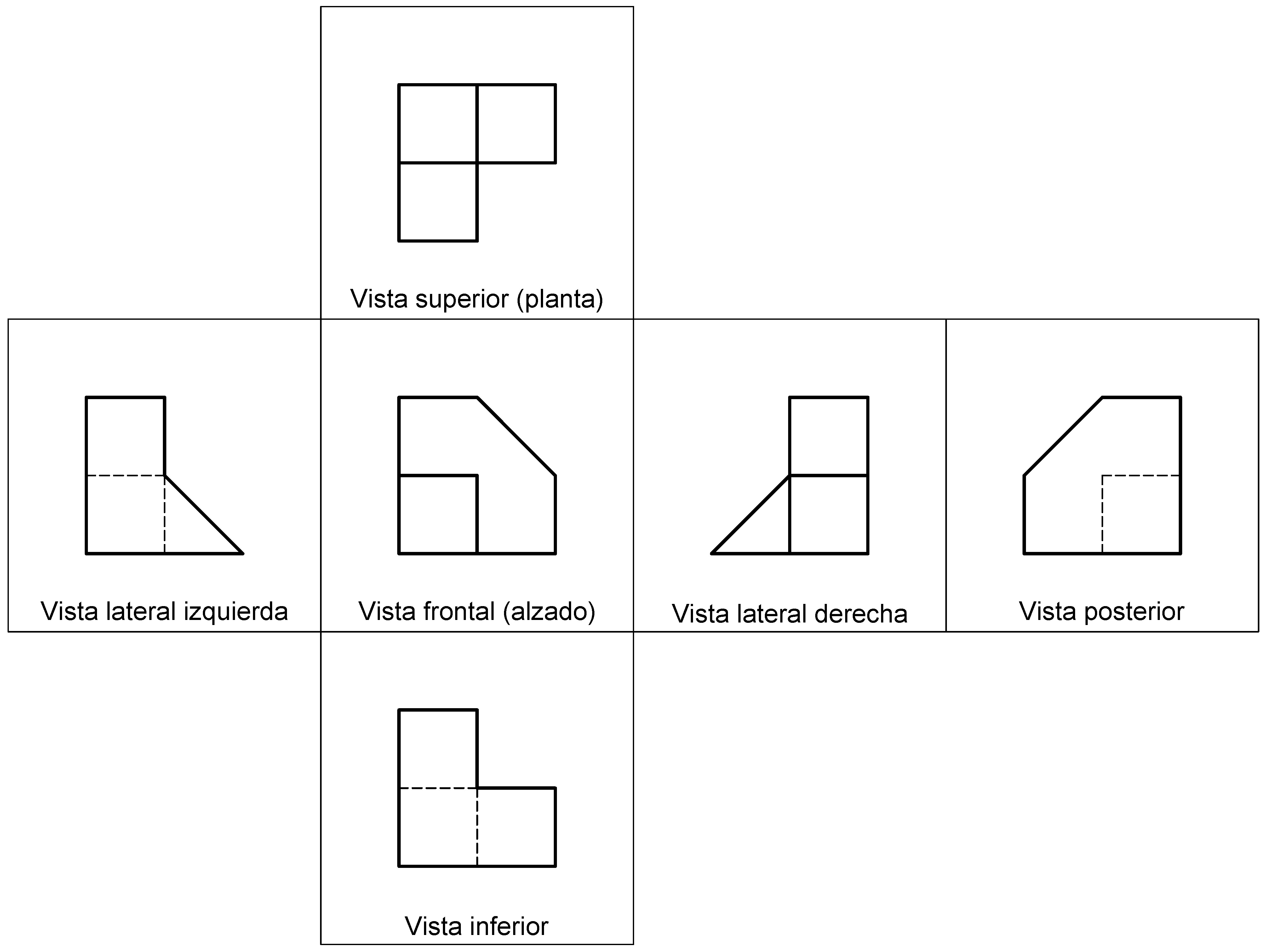
Se conoce por vistas normalizadas de una pieza sus proyecciones ortogonales sobre las caras de un paralelepípedo que la envuelve, cuyas caras son paralelas a los planos del sistema de referencia de la pieza.

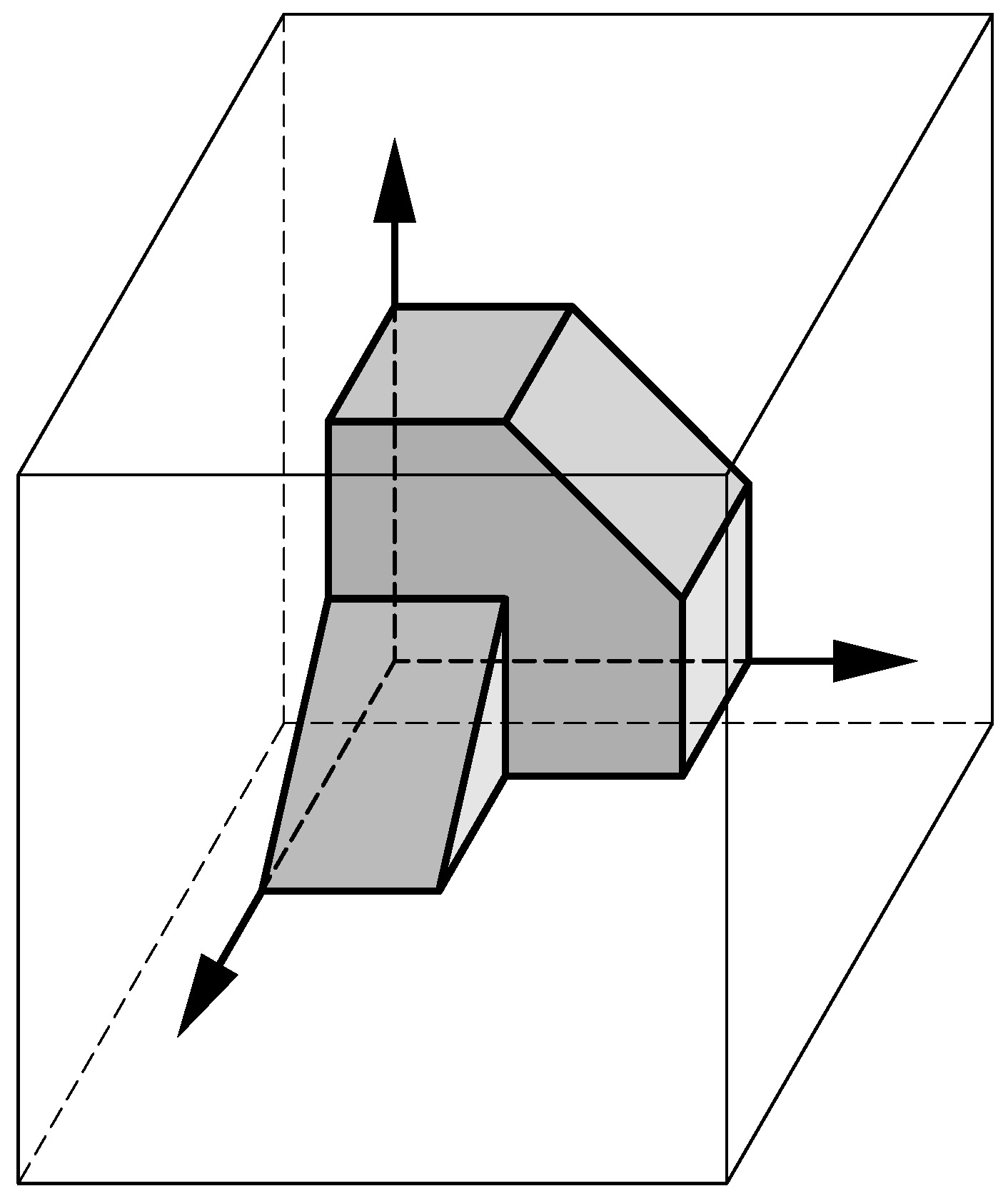
Figura 4.1.

Estas proyecciones ortogonales se realizan según dos sistemas:

1. Sistema de proyección del primer diedro (antiguamente denominado Sistema Europeo): la pieza se sitúa entre el punto de vista (situado en el infinito) y la cara del paralelepípedo sobre la que se proyecta.
2. Sistema de proyección del tercer diedro (antiguamente denominado Sistema Americano): la pieza se sitúa por detrás de la cara del paralelepípedo sobre la que se proyecta.

En las proyecciones se distinguen las aristas visibles desde el punto de vista (con trazo continuo), de aquéllas que quedan ocultas por la propia pieza (trazo discontinuo).

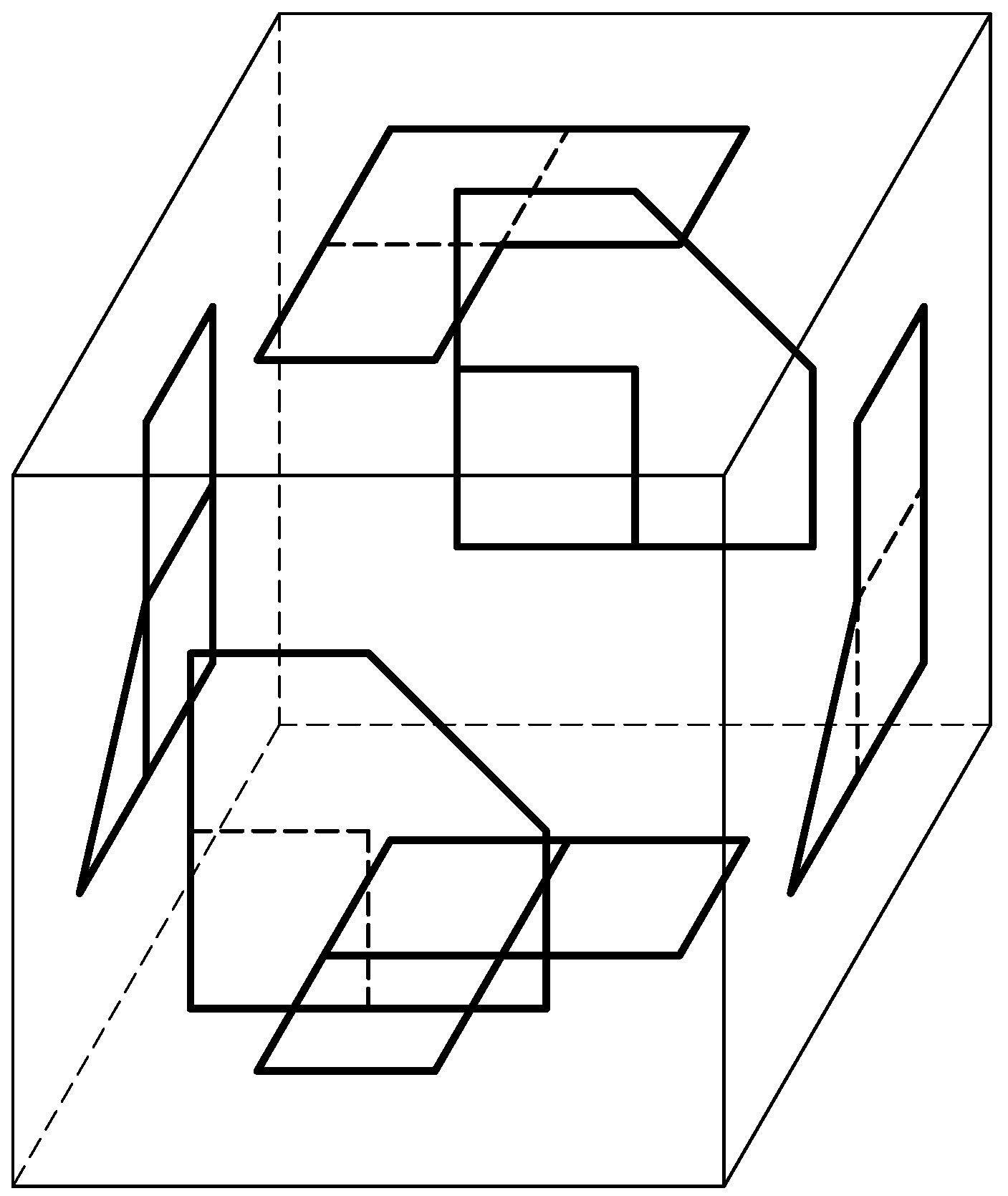
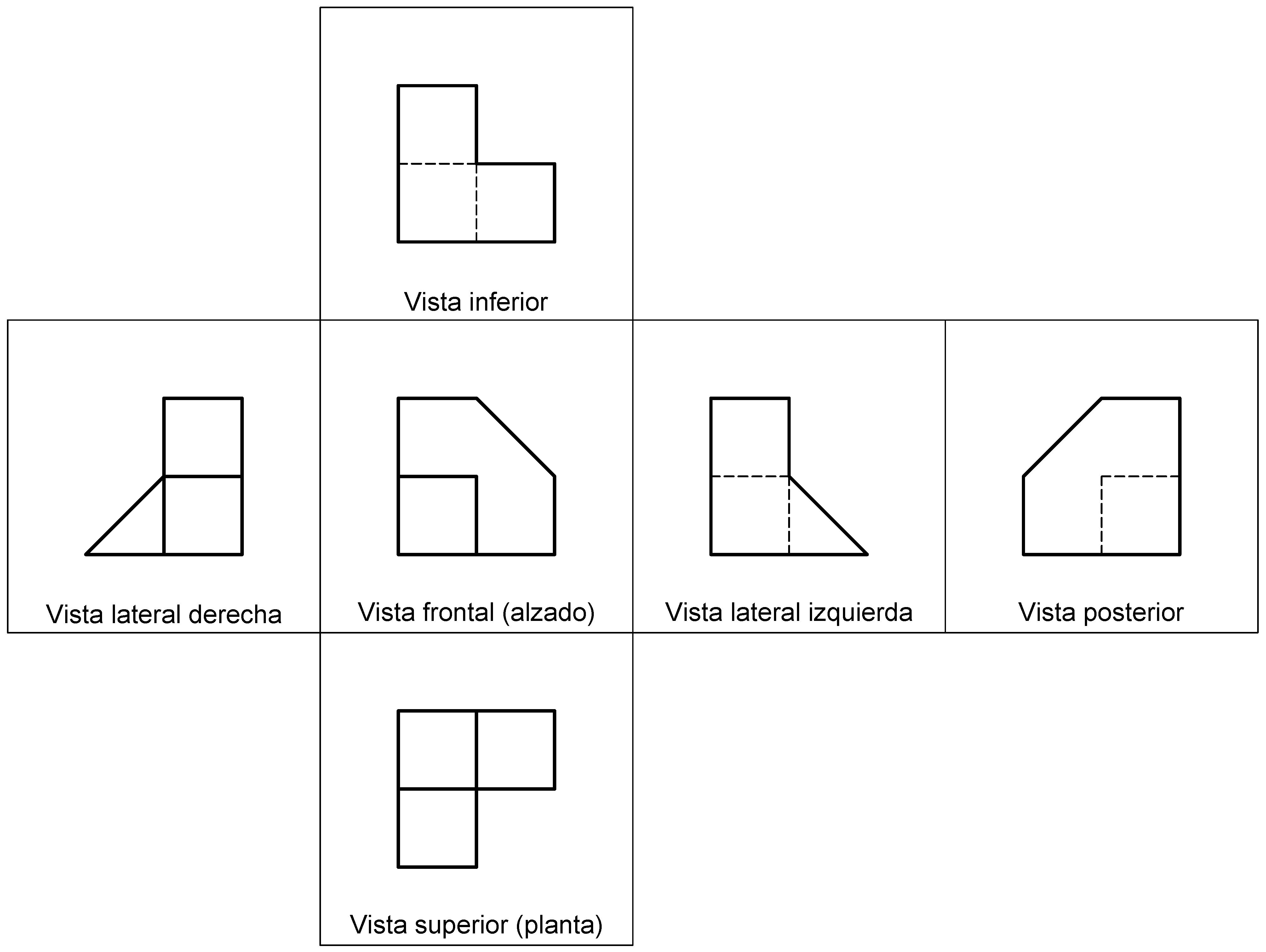
Una vez efectuadas estas proyecciones se abaten las caras del paralelepípedo sobre el plano de la cara correspondiente al alzado, quedando ordenadas las vistas normalizadas de la pieza de la forma indicada en las figuras siguientes.

Las caras del objeto representado paralelas a la del paralelepípedo de proyección se observan en verdadera magnitud en sus proyecciones sobre éstas.

SISTEMA DE PROYECCIÓN DEL PRIMER DIEDRO	SISTEMA DE PROYECCIÓN DEL TERCER DIEDRO

Para evitar confusiones en la lectura de los planos es necesario identificar el sistema de proyección empleado. Ello se realiza añadiendo a las vistas normalizadas uno de los símbolos indicados en la figura siguiente, correspondientes al alzado y vista lateral derecha de sendos troncos de cono idénticos representados en ambos sistemas de proyección:

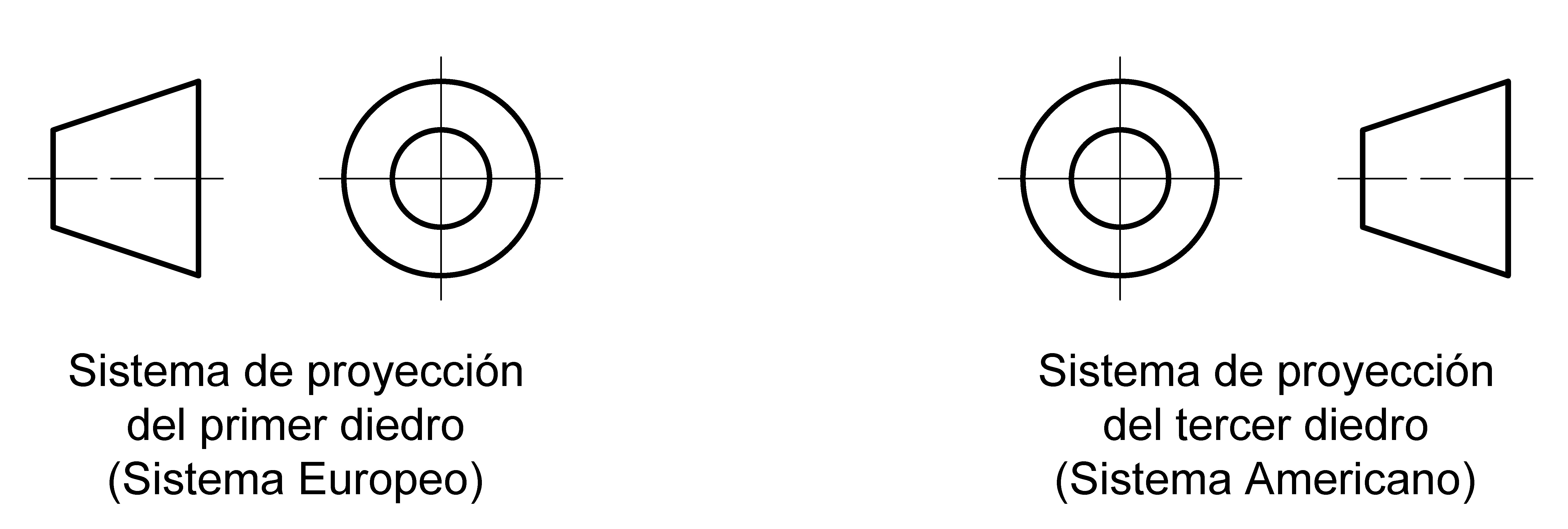
Figura 4.8.

Una única vista no define geométricamente un cuerpo. La proyección de un punto cualquiera sobre un plano no difiere de la de cualquier otro punto alineado con él y con el punto de vista. De igual forma, todas las rectas contenidas en un plano que contenga al punto de vista tienen la misma proyección. Según la imagen de la izquierda¹ una mujer sostiene la Torre de Pisa, la cual se está viniendo abajo. Eso ocurre porque las palmas de sus manos y el contorno de la torre están alineados con el objetivo de la cámara fotográfica. Evidentemente si se observara esa realidad desde otro punto de vista se vería algo parecido a la imagen de la derecha².

Figura 4.9.

Figura 4.10.

Son necesarias dos o tres vistas de un cuerpo para definirlo geométricamente. En la figura siguiente se muestran las vistas de planta y alzado de dos cuerpos, según el sistema de representación del primer diedro de proyección. El cuerpo de la izquierda queda perfectamente determinado con estas dos vistas; se trata de una pirámide de base cuadrada. Sin embargo, las dos vistas dadas del cuerpo de la derecha no lo definen. Dichas vistas pueden corresponder, entre otros cuerpos, a un cubo, a una cuña triangular, a un cilindro, etc.

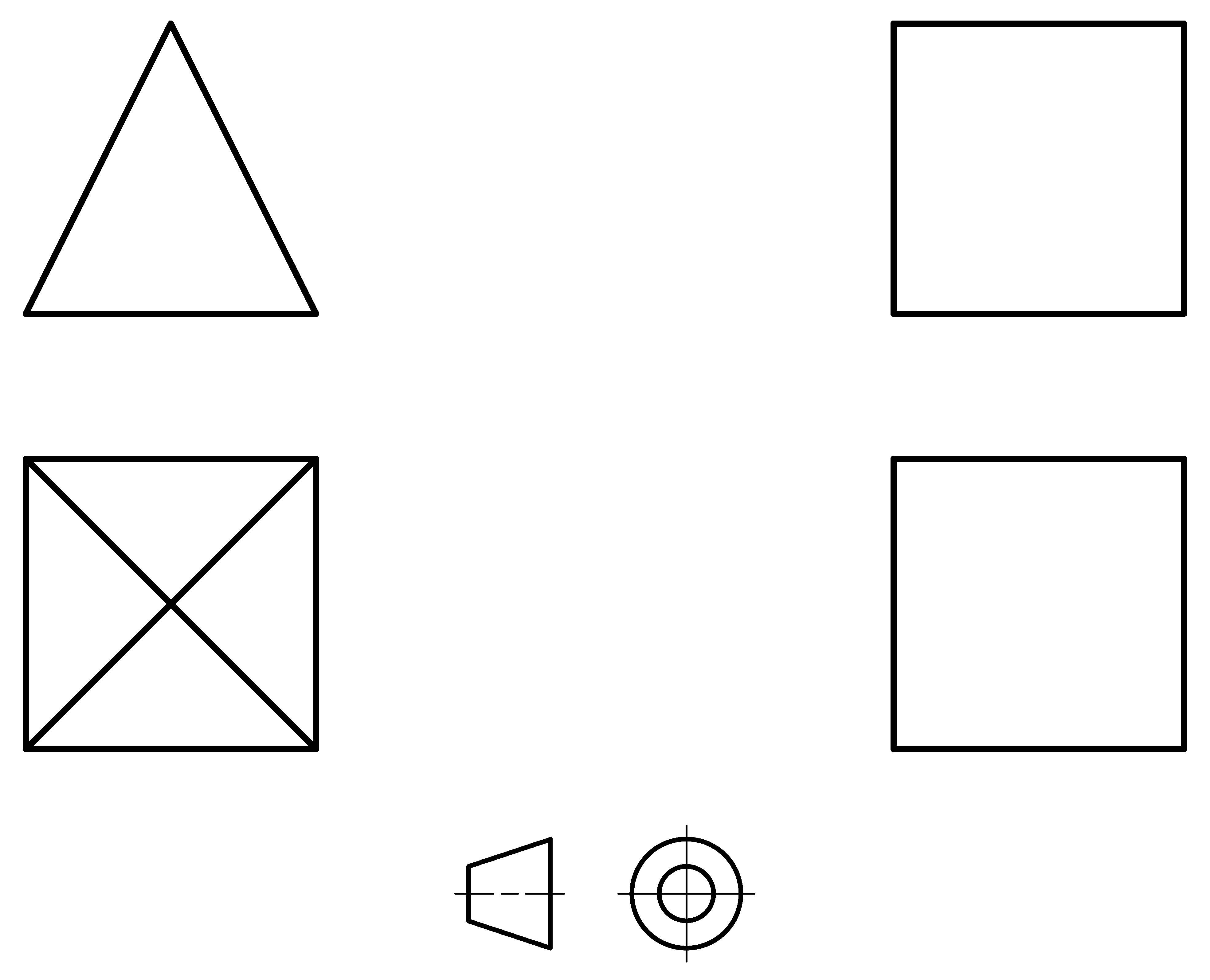
Figura 4.11.

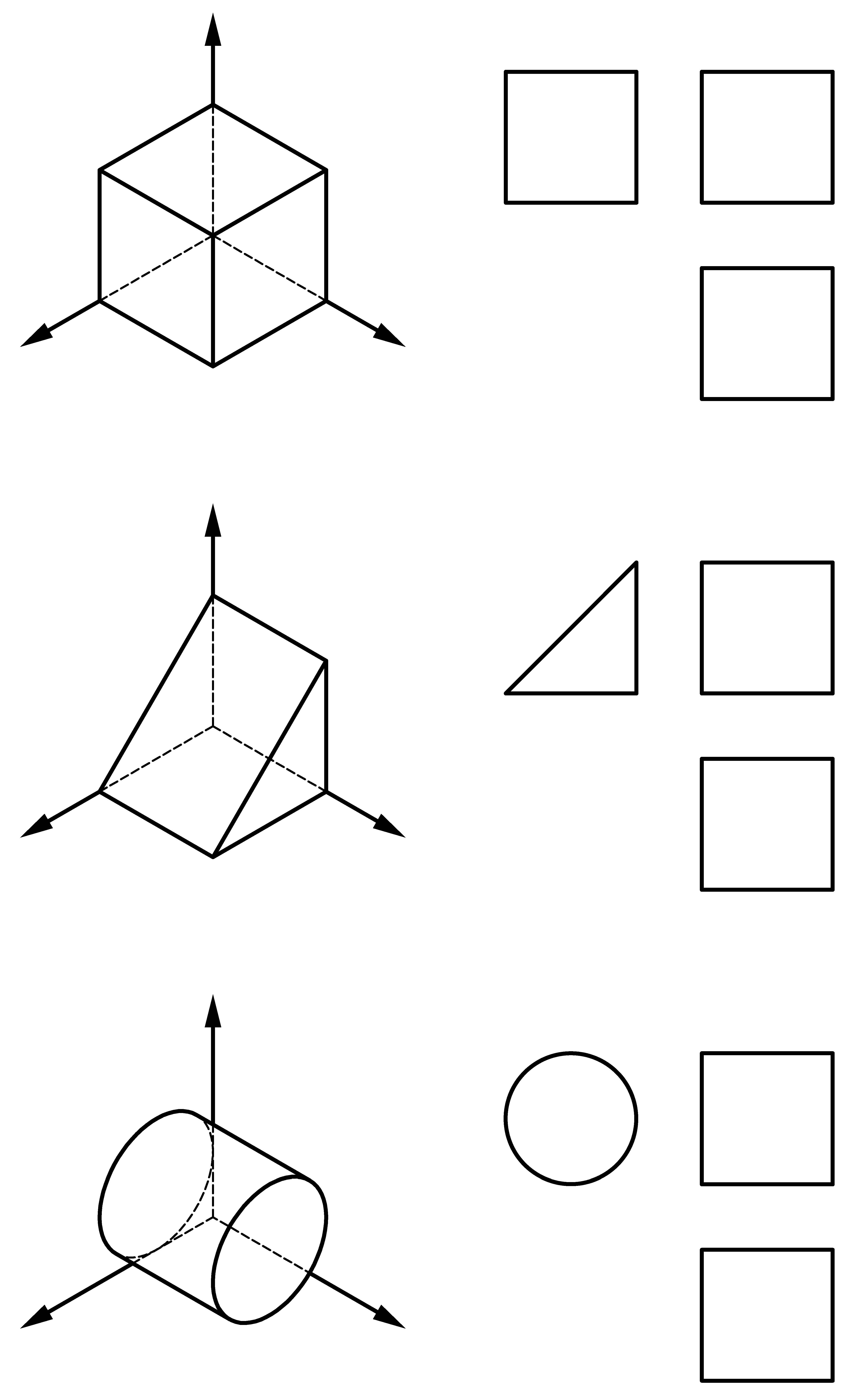
Figura 4.12.

1 Barney Moss (2013). Pushing the Leaning Tower of Pisa – 3. https://www.flickr.com/photos/barneymoss (accedido 11/07/2016).

2 Roberto Venturini (2009). P1080552. https://www.flickr.com/photos/robven/ (accedido 11/07/2016).

La perspectiva o las vistas normalizadas de un cuerpo que se dibujen sobre el papel deben estar representadas con unas dimensiones que faciliten la lectura y comprensión por otras personas, y que se adapten al tamaño del formato de papel sobre el que se van a dibujar. Estas dimensiones no suelen corresponder con las propias del objeto, por lo que es necesario aplicar un factor de escala (e), que se define como el cociente entre lo que mide un elemento en el dibujo (m) y lo que el mismo elemento mide en la realidad (n), es decir, e = m:n. El factor de escala puede ser de ampliación si el objeto a representar es muy pequeño, o de reducción si es muy grande.

Las normas recomiendan usar factores de escala en los que el denominador o el numerador sean la unidad (escala de ampliación en el primer caso, y de reducción en el segundo), y el otro término del cociente sea 2, 5, 10 o múltiplos de éstos:

• Ampliación: 2:1, 5:1, 10:1, 20:1, 50:1, 100:1, etc.
• Reducción: 1:2, 1:5, 1:10, 1:20, 1:50, 1:100, 1:200, 1:500, 1:1.000, etc.

La aplicación de los factores de escala se realiza de la siguiente forma:

1. Dibujo de las vistas normalizadas de un cuerpo conociendo las dimensiones de éste:
   
   Sea e_vistas la escala a la que se pretenden dibujar las vistas normalizadas de un determinado cuerpo. La medida con la que se han de representar en una vista concreta las aristas del objeto paralelas al plano de dicha vista es el producto de su medida real por el factor de escala: L_vista = L_real × e_vistas.
   
   
2. Obtención de las dimensiones de un cuerpo a partir de sus vistas normalizadas:
   
   Se trata de la operación inversa a la anterior. La longitud de una arista paralela al plano de una de las vistas normalizadas se obtiene a partir de su medida en ésta dividiéndola por el factor de escala: L_real = L_vista / e_vistas = L_vista × (e_vistas)^-1.
   
   
3. Dibujo de la perspectiva de un cuerpo conociendo las dimensiones de éste:
   
   Sea epersp la escala a la que se pretende dibujar la perspectiva del cuerpo, y ηx, ηy y ηz los coeficientes de reducción en los tres ejes coordenados correspondientes al tipo de perspectiva a emplear (por ejemplo, en perspectiva caballera ηx = ηz = 1 y ηy es variable, y en perspectiva isométrica ηx = ηy = ηz ≈ 0,8). Tres aristas paralelas a los ejes coordenados y de longitudes reales L_x,real, L_y,real y L_z,real se deberán representar con las medidas dadas por las expresiones siguientes, respectivamente:
   
   L_x,persp = L_x,real × e_persp × η_x
   L_y,persp = L_y,real × e_persp × η_y
   L_z,persp = L_z,real × e_persp × η_z
   
   
4. Obtención de las dimensiones de un cuerpo a partir de una perspectiva:
   
   Se aplican las fórmulas anteriores despejando las longitudes reales:
   
   L_x,real = L_x,persp × (e_persp)^-1 / η_x
   L_y,real = L_y,persp × (e_persp)^-1 / η_y
   L_z,real = L_z,persp × (e_persp)^-1 / η_z
   
   
5. Dibujo de las vistas normalizadas de un cuerpo a partir de una perspectiva:
   
   Se trata en primer lugar de determinar las medidas reales del cuerpo a partir de su perspectiva (caso d), y dibujar a continuación sus vistas normalizadas (caso a):
   
   L_x,vista = L_x,real × e_vistas = (L_x,persp × (e_persp)^-1 / η_x) × e_vistas
   L_y,vista = L_y,real × e_vistas = (L_y,persp × (e_persp)^-1 / η_y) × e_vistas
   L_z,vista = L_z,real × e_vistas = (L_z,persp × (e_persp)^-1 / η_z) × e_vistas
   
   
6. Dibujo de la perspectiva de un cuerpo a partir de sus vistas normalizadas:
   
   Se obtienen en primer lugar las medidas reales del cuerpo a partir de sus vistas (caso b), y con ellas se dibuja su perspectiva (caso c):
   
   L_x,persp = L_x,real × e_persp × η_x = (L_x,vista × (e_vistas)^-1) × e_persp × η_x
   L_y,persp = L_y,real × e_persp × η_y = (L_y,vista × (e_vistas)^-1) × e_persp × η_y
   L_z,persp = L_z,real × e_persp × η_z = (L_z,vista × (e_vistas)^-1) × e_persp × η_z