Una carga \(q=-2\mu\)C situada inicialmente en el origen se dirige en el sentido positivo del eje OY con velocidad 2 m/s.

Calcular el campo generado por dicha carga en el punto de coordenadas (1,1,0) en el instante inicial.

Calcular el campo generado por la misma carga en el mismo punto 1 s después.

SOLUCIÓN:

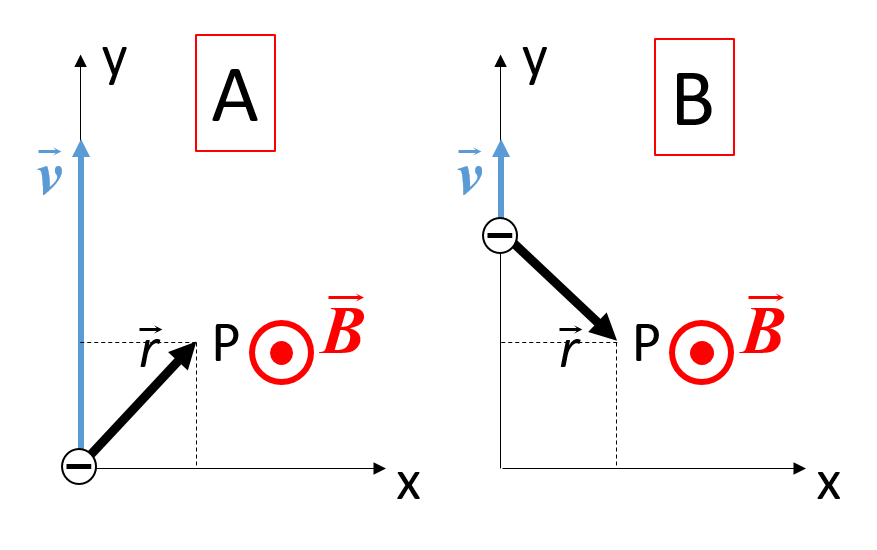
Para calcular el campo magnético debemos usar la expresión:
\[\vec{B}=\frac{\mu}{4\pi}\frac{q}{r^3}\vec{v}\times\vec{r}\]
siendo \(\mu=4\pi\cdot 10^{-7}\) N/A\(^2\), \(q=-2\times 10^{-6}\) C y \(\vec{v}=2\hat{\jmath}\) m/s. Finalmente \(\vec{r}\) es el vector que comienza en la carga (cuya posición es \(\vec{r}_q\)) y acaba en el punto de interés (de posición \(\vec{r}_P\)). Este vector varía según la posición de la carga:
\[\vec{r}=\vec{r}_P-\vec{r}_q\]
En la figura A se muestra un esquema de la situación inicial. En este caso, \(\vec{r}_q=0\), y \(\vec{r}_P=(\hat{\imath}+\hat{\jmath})\) m, por lo que
\[\vec{r}=(\hat{\imath}+\hat{\jmath})\mbox{ m}\]
y su módulo es \(r=\sqrt{2}\). Por lo tanto:
\[\vec{B}=\frac{4\pi\cdot 10^{-7}\mbox{ N/A}^2}{4\pi}\frac{-2\times 10^{-6}\mbox{ C}}{(\sqrt{2})^3\mbox{ m}^3}2\hat{\jmath}\mbox{ m/s}\times(\hat{\imath}+\hat{\jmath})\mbox{ m}\] \[\vec{B}=\sqrt{2}\cdot 10^{-13}\hat{k}\mbox{ T}\]
1 segundo después nos encontraremos en la situación de la figura B, la carga se sitúa en un punto diferente: \(\vec{r}_q=\vec{v}t=2\hat{\jmath}\) m, por lo tanto:
\[\vec{r}=\vec{r}_P-\vec{r}_q=\hat{\imath}-\hat{\jmath}\mbox{ m}\]
Y el campo magnético será:
\[\vec{B}=\frac{4\pi\cdot 10^{-7}\mbox{ N/A}^2}{4\pi}\frac{-2\times 10^{-6}\mbox{ C}}{(\sqrt{2})^3\mbox{ m}^3}2\hat{\jmath}\mbox{ m/s}\times(\hat{\imath}-\hat{\jmath})\mbox{ m}\] \[\vec{B}=\sqrt{2}\cdot 10^{-13}\hat{k}\mbox{ T}\]

EJERCICIOS DE CAMPOS CREADOS POR CARGAS EN MOVIMIENTO