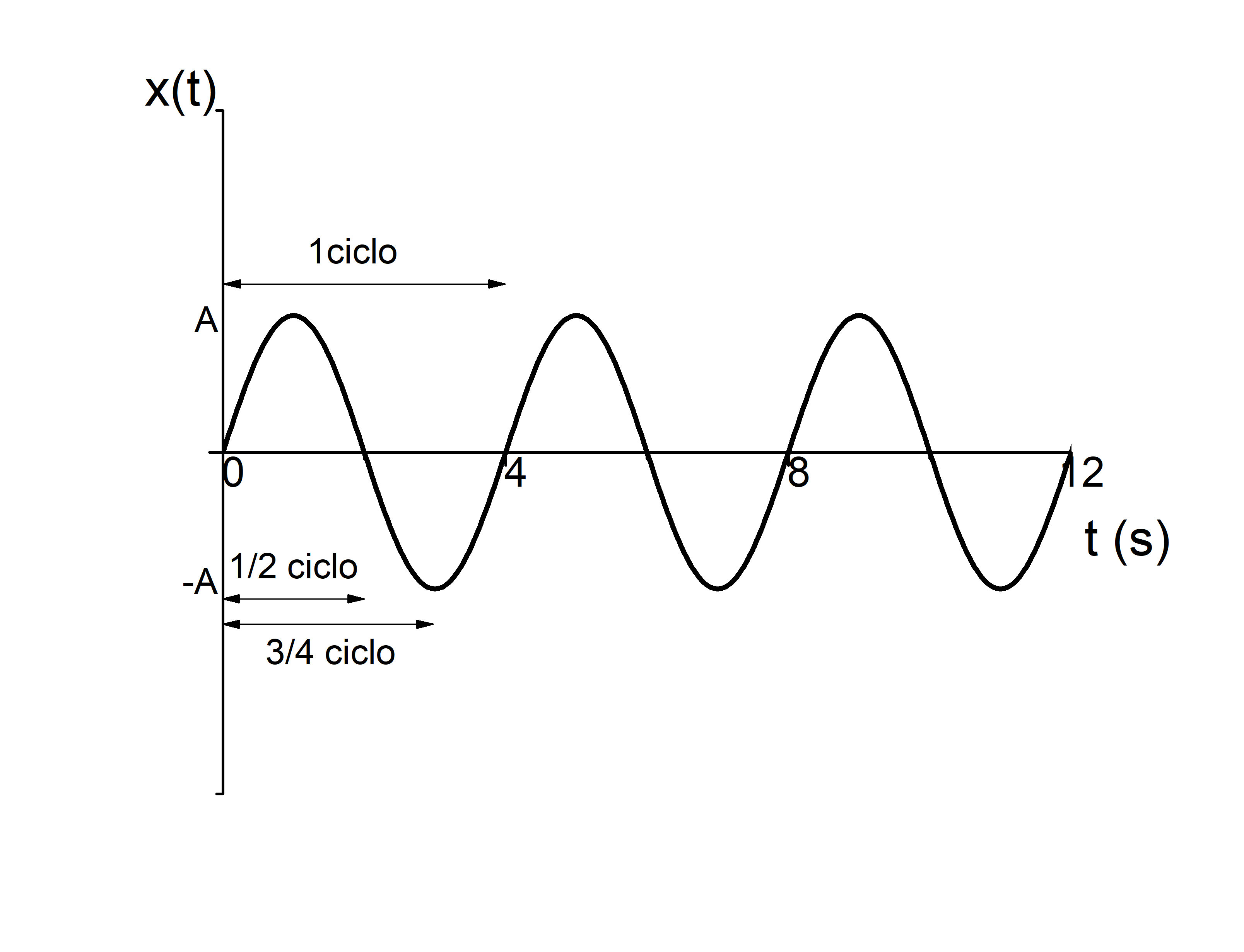
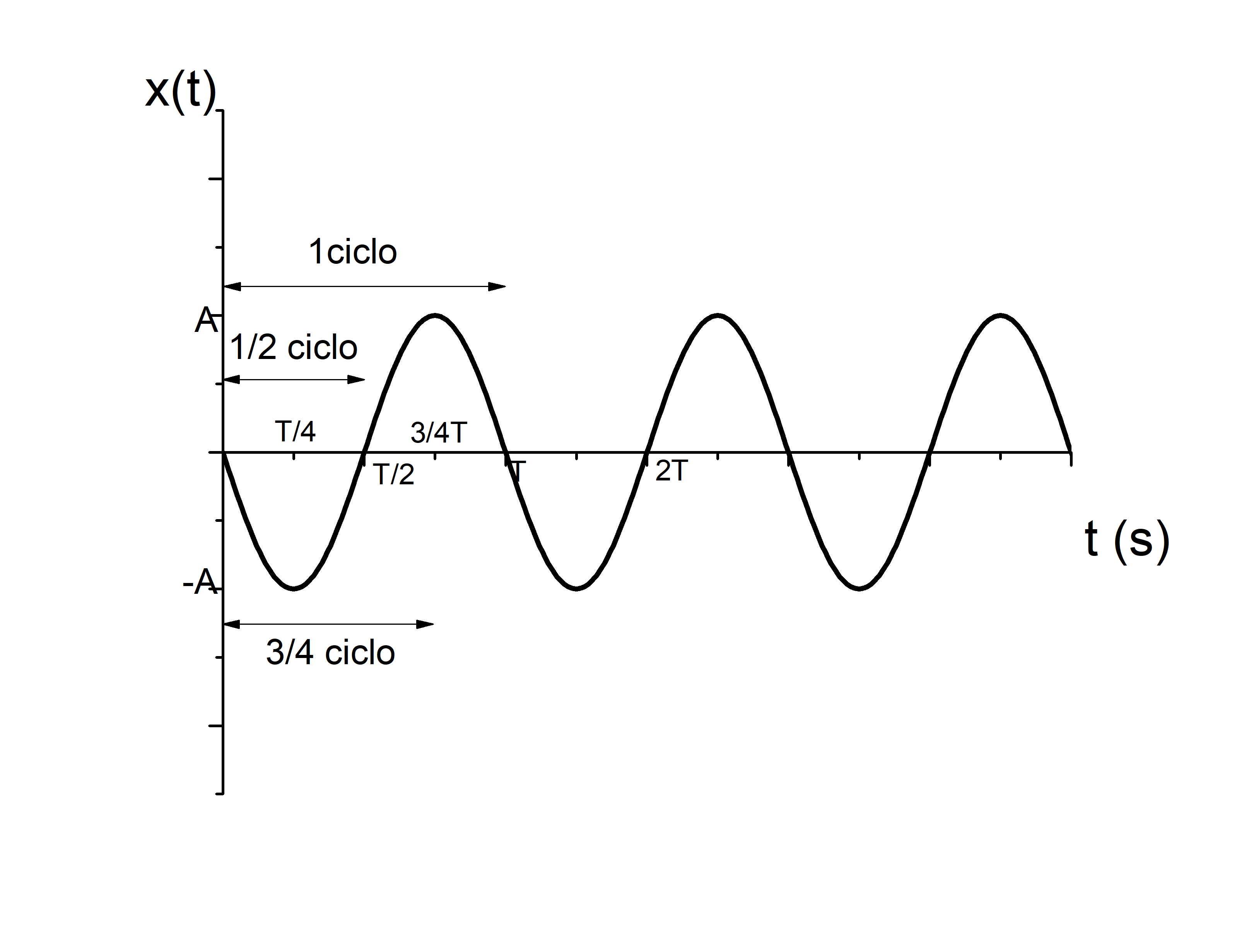
Un M.A.S. viene descrito por la siguiente ecuación: \(x(t)=3\sin\left(2\pi 1000 t+\pi/2\right)\mbox{ m}\). Calcule el periodo, la frecuencia, la frecuencia angular y la amplitud del movimiento.
Un M.A.S. viene descrito por la siguiente ecuación: \(x(t)=2.5\cos\left(800 t+\pi/2\right)\mbox{ m}\). Calcule el periodo, la frecuencia, la frecuencia angular y la amplitud del movimiento.
Un M.A.S. viene descrito por la siguiente ecuación: \(x(t)=82\cos\left(\frac{2\pi}{2.5} t+\pi/2\right)\mbox{ m}\). Calcule el periodo, la frecuencia, la frecuencia angular y la fase inicial del movimiento.
Una partícula describe un M.A.S. con una amplitud de 3 m y una frecuencia de 25 Hz. En el instante inicial, la partícula se encuentra en \(x=2 \text{ m}\). Calcular la fase inicial y la posición en el instante \(t=3 \text{ s}\).
Una partícula describe un M.A.S. con una amplitud de 3 m y una frecuencia de 0.25 Hz. En el instante inicial, la partícula se encuentra en el origen \(x=0\) y con velocidad positiva. Calcular la posición en el instante \(t=3 \text{ s}\). Repetir el cálculo para el caso en el que la velocidad inical sea negativa.
Una cuerda de \(R= 2 \text{ m}\) de largo está fija en un extremo. En el extremo contrario hay una masa que describe círculos a velocidad constante, de modo que tarda 2 s en dar una vuelta completa. Describa la evolución temporal de la componente \(x\) de su posición. Calcule el periodo, la frecuencia, la frecuencia angular y la amplitud del movimiento.