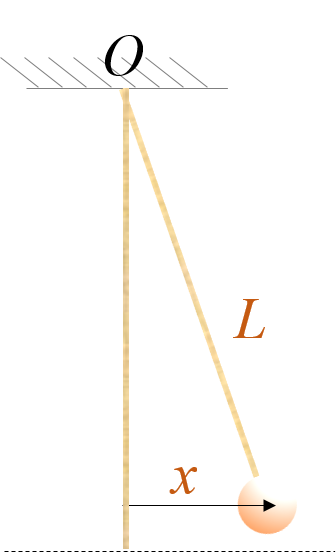Una masa de 50 g está sujeta a un muelle horizontal de constante \(k=25 \text{ N/m}\). Calcule el periodo de las oscilaciones.
SOLUCIÓN:
Dado que \(\omega=\sqrt{\frac{k}{m}}\), por lo que \[T=\frac{2\pi}{\omega}=\frac{2\pi}{\sqrt{\frac{k}{m}}}=\frac{2\pi}{\sqrt{\frac{25\mbox{ N/m}}{0.05\mbox{ kg}}}}=\boxed{0.28\mbox{ s}}\]
Se hace oscilar horizontalmente una masa de 0.5 kg sujeta a un muelle de constante desconocida. Se observa que en un minuto realiza 45 oscilaciones. Calcule la constante del muelle.
SOLUCIÓN:
Para conocer la constante del muelle, recuérdese que la periodicidad de las oscilaciones está relacionada con dicha constante y con la masa oscilante a través de \(\omega=\sqrt{\frac{k}{m}}\), por lo que \[k=m\omega^2\] Para calcular la frecuencia angular, fíjese que nos dan el número de oscilaciones \(N=45\) en un minuto, podemos calcular el número de oscilaciones en 1 s, es decir, la frecuencia, como: \[f=\frac{45}{60\mbox{ s}}=0.75\mbox{ Hz}\] Por lo que \(\omega=2\pi f=1.5\pi \text{ rad/s}\) y finalmente: \[k=0.5(1.5\pi)^2=\boxed{11.1\mbox{ N/m}}\]
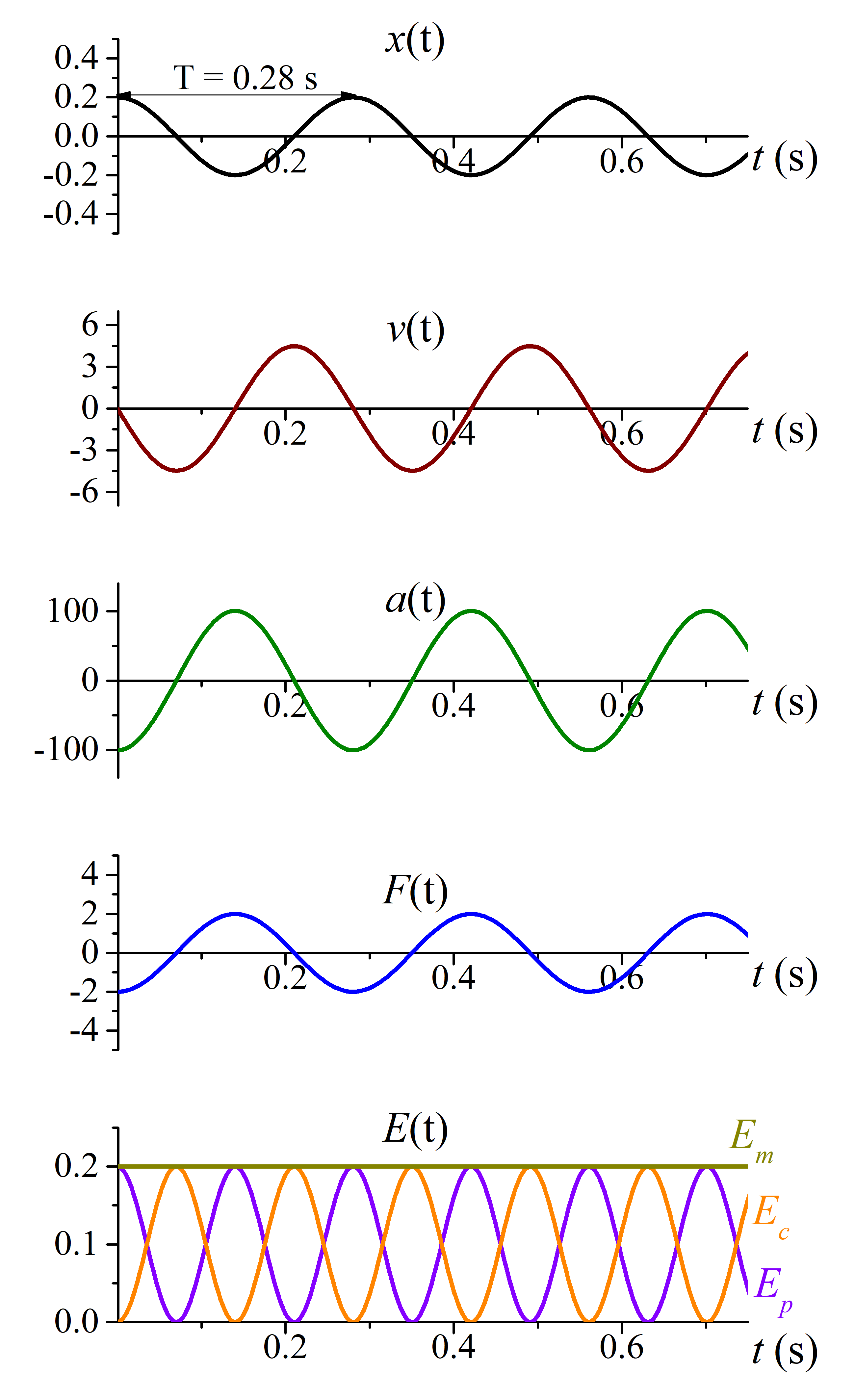
Una masa de 20 g está en el origen y sujeta a un muelle horizontal de constante \(k=10 \text{ N/m}\). En el instante inicial se coloca la masa en la posición \(x=-20 \text{ cm}\) y se suelta. Escriba la ecuación que describe la posición en función del tiempo, la velocidad, la aceleración, la fuerza ejercida por el muelle, su energía potencial, la energía cinética de la masa y la energía mecánica. Represente gráficamente cada una de estas funciones.
SOLUCIÓN:
Con las características de este sistema, la frecuencia angular será: \[\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{10}{0.02}}=22.4\mbox{ rad/s}\] Y el periodo será: \[T=\frac{2\pi}{\omega}=\frac{2\pi}{22.4\mbox{ rad/s}}=0.28\mbox{ s}\] La forma general del movimiento es: \[x(t)=A\sin\left(\omega t+\varphi_0\right)\] Y su velocidad: \[v(t)=\omega A\cos\left(\omega t+\varphi_0\right)\] En el instante inicial se suelta la masa, luego en ese instante su velocidad es cero: \[v(0)=\omega A\cos\left(\varphi_0\right)=0\] Dado que ni \(\omega\) ni \(A\) pueden ser cero (pues en ese caso no habría movimiento), entonces, \[\cos\left(\varphi_0\right)=0\] Lo cual se cumple siempre y cuando \[\varphi_0=\pi/2\] Por otro lado, me dicen que en el instante inicial la partícula está en \(x(0)=0.2 \text{ m}\), luego: \[x(0)=A\sin\left(\varphi_0\right)=A\sin\left(\pi/2\right)=A=0.2\mbox{ m}\]
Por lo tanto: \[\boxed{x(t)=0.2\sin\left(22.4 t+\pi/2\right)\text{ m}}\] La amplitud de la velocidad es \(\omega A=22.4\mbox{ rad/s}\cdot 0.2\mbox{ m}=4.48 \text{ m/s}\), y por lo tanto \[\boxed{v(t)=4.48\cos\left(22.4 t+\pi/2\right)\mbox{ m/s}}\]
La aceleración la podemos calcular como la derivada temporal de la velocidad: \[a(t)=\frac{dv}{dt}=-\omega^2A\sin\left(\omega t+\varphi_0\right)\] Y la amplitud de la aceleración será \(\omega^2A=(22.4\mbox{ rad/s})^2\cdot0.2\mbox{ m}=100.4 \text{ m/s}^2\), por lo que: \[a(t)=\frac{dv}{dt}=\boxed{-100.4\sin\left(22.4 t+\pi/2\right)\mbox{ m/s}^2}\]
Para calcular la fuerza podemos hacer uso de dos ecuaciones: \[F=-kx(t)=-kA\sin\left(\omega t+\varphi_0\right)\] o bien \[F(t)=ma(t)=-m\omega^2A\sin\left(\omega t+\varphi_0\right)\] lo cual da el mismo resultado. La amplitud de la fuerza será \(m\omega^2A=kA=2 \text{ N}\), por lo que \[\boxed{F(t)=-2\sin\left(22.4 t+\pi/2\right)\mbox{ N}}\]
La energía potencial viene dada por \(E_p(t)=\frac{1}{2}kx(t)^2\), por lo que \[E_p(t)=\frac{1}{2}k\bigl[A\sin\left(\omega t+\varphi_0\right)\bigr]^2\] Sustituyendo los valores calculados: \[\boxed{E_p(t)=0.2\sin^2\left(22.4 t+\pi/2\right)\mbox{ J}}\]
La energía cinética se calcula como \(E_c(t)=\frac{1}{2}mv(t)^2\), por lo que: \[E_c(t)=\frac{1}{2}m\omega^2\bigl[A\cos\left(\omega t+\varphi_0\right)\bigr]^2\] Sustituyendo: \[\boxed{E_c(t)=0.2\mbox{ J}\cos^2\left(22.4 t+\pi/2\right)}\]
La energía mecánica \(E_m=E_p+E_c\) se conserva y por lo tanto no varía con el tiempo. Podemos utilizar cualquier instante para calcularlo, por ejemplo el instante en que \(E_c=0\). Vimos que en ese instante, la energía potencial es máxima, por lo tanto \(E_p=0.2 \text{ J}\). Entonces, \[\boxed{E_m=0.2\mbox{ J}}\]
Fíjese que dado que las amplitudes de la energía potencial y cinética son iguales. Esto debe ser así, ya que la energía mecánica coincide con el máximo de cualquiera de ellas.
En la siguiente figura se representan estas funciones:
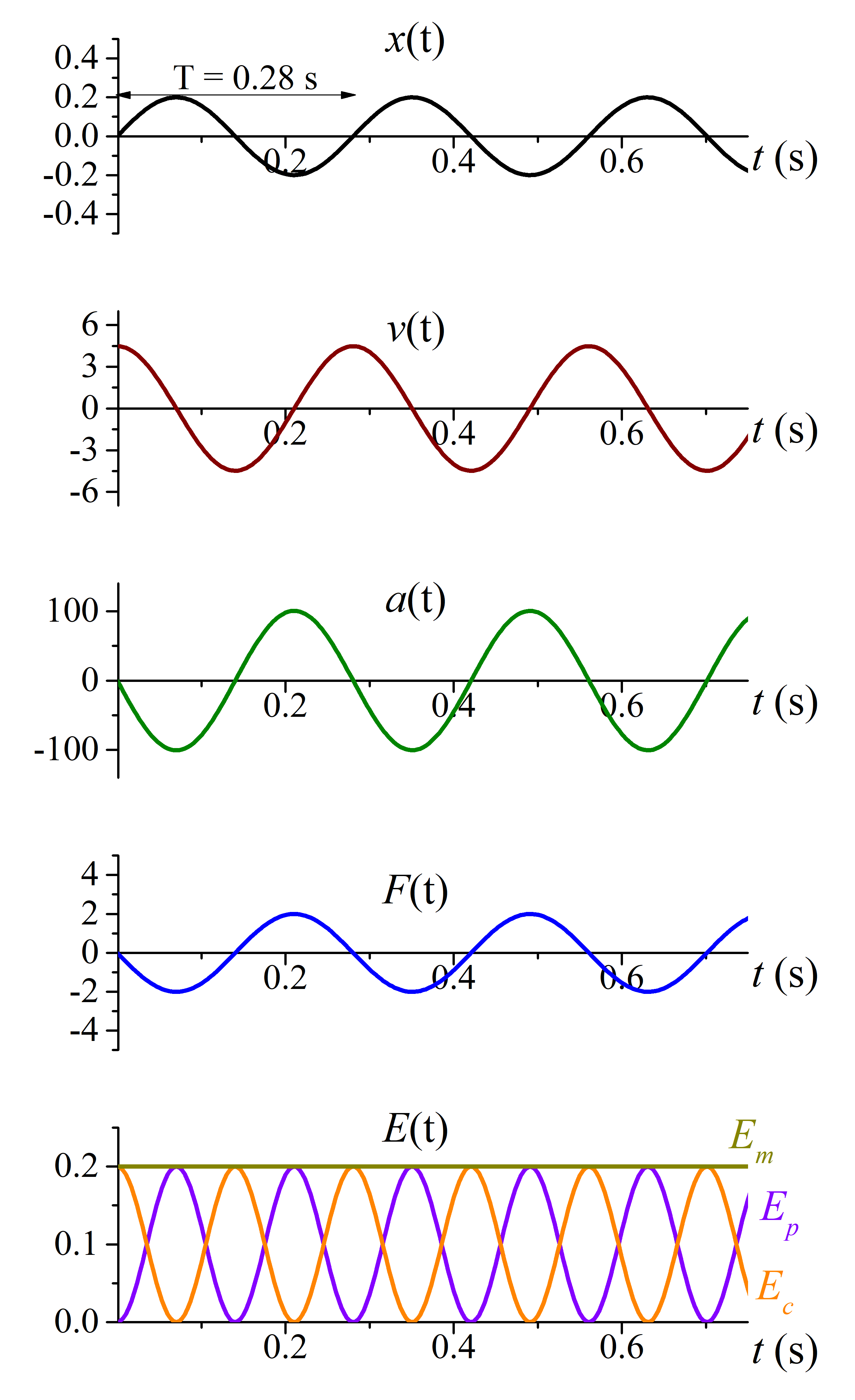
Una masa de 20 g está en el origen y sujeta a un muelle horizontal de constante \(k=10 \text{ N/m}\). En el instante inicial se coloca la masa en la posición de equilibrio y se le imprime una velocidad de 4.48 m/s. Escriba la ecuación que describe la posición en función del tiempo, la velocidad, la aceleración, la fuerza ejercida por el muelle, su energía potencial, la energía cinética de la masa y la energía mecánica. Represente gráficamente cada una de estas funciones.
SOLUCIÓN:
Este problema cambia respecto al anterior puesto que las condiciones iniciales (posición y velocidad iniciales) son diferentes.
Con las características de este sistema, la frecuencia angular será igual que en el problema anterior: \[\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{10}{0.02}}=22.4\mbox{ rad/s}\] Y el periodo será: \[T=\frac{2\pi}{\omega}=\frac{2\pi}{22.4\mbox{ rad/s}}=0.28\mbox{ s}\] La forma general del movimiento es: \[x(t)=A\sin\left(\omega t+\varphi_0\right)\] Y su velocidad: \[v(t)=\omega A\cos\left(\omega t+\varphi_0\right)\] Pero en este caso, en el instante inicial la masa está en la posición de equilibrio. Esto quiere decir que: \[x(0)=0=A\sin\left(\varphi_0\right)\] Condición que se cumple si \(\varphi_0=0\). Por otro lado, la velocidad inicial es 4.48 m/s, es decir \[v(0)=4.48=\omega A\cos\left(\varphi_0\right)=\omega A\] donde se ha utilizado que \(\cos\left(\varphi_0\right)=\cos 0=1\). Como \(\omega=22.4 \text{ rad/s}\), entonces: \[A=\frac{v(0)}{\omega}=\frac{4.48\mbox{ m/s}}{22.4\mbox{ rad/s}}=0.2\mbox{ m}\] Por lo tanto: \[\boxed{x(t)=0.2\sin\left(22.4 t\right)\mbox{ m}}\] \[\boxed{v(t)=4.48\cos\left(22.4 t\right)\mbox{ m/s}}\] Vemos que la solución es la misma, pero con una fase inicial \(\varphi_0=0\), por lo que: \[\boxed{a(t)=-100.4\sin\left(22.4 t\right)\mbox{ m/s}^2}\] \[\boxed{F(t)=-2\sin\left(22.4 t\right)\mbox{ N}}\] \[\boxed{E_p(t)=0.2\sin^2\left(22.4 t\right)\mbox{ J}}\] \[\boxed{E_c(t)=0.2\cos^2\left(22.4 t\right)\mbox{ J}}\] \[\boxed{E_m=0.2\mbox{ J}}\]
En la siguiente figura se representan estas funciones:
En estas figuras vemos que la diferencia fundamental es el momento del ciclo en el que comienza la oscilación.
A un resorte, cuya longitud natural, cuando está colgado de un punto fijo es de 25 cm, se le cuelga una masa de 80 g, unida a su extremo libre. Cuando esta masa está en posición de equilibrio, la longitud del resorte es de 33 cm. La masa se impulsa 8 cm hacia abajo y se suelta. Calcule:
La constante recuperadora del muelle.
Las expresiones de la elongación y de la velocidad, tomando como referencia la posición de equilibrio de resorte-masa.
Los valores máximos de las magnitudes anteriores.
SOLUCIÓN:
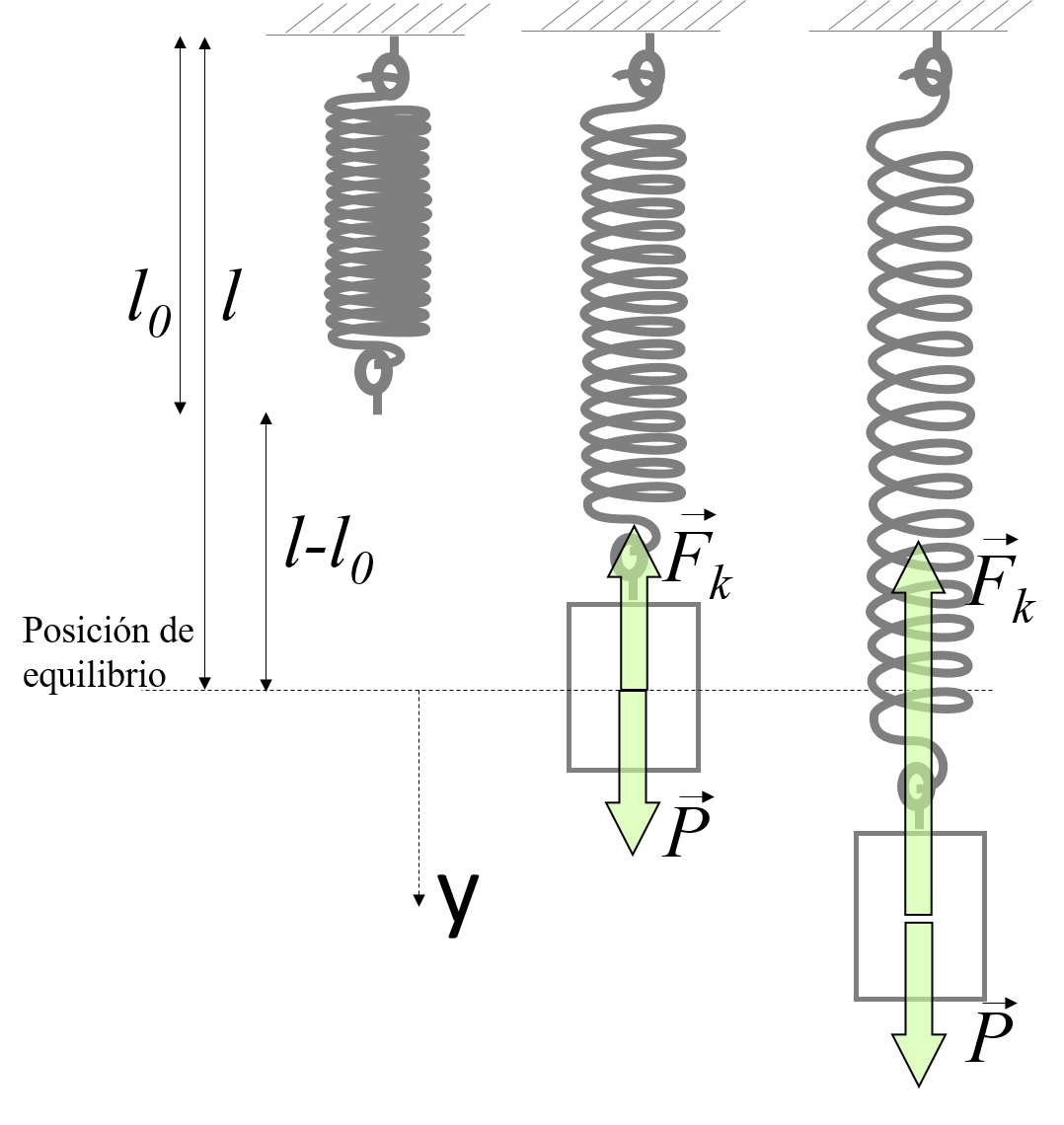
En este caso, el sistema está en posición vertical, por lo que además de la fuerza del muelle tendremos la fuerza gravitatoria. Esto se muestra en el siguiente esquema:
En el segundo dibujo, el objeto está en equilibrio. Por lo tanto, \[\sum\vec{F}=0\] Las fuerzas que actúan son la fuerza del muelle \(\vec{F}_k=-k(l-l_0)\hat{\jmath}\) y la fuerza gravitatoria \(\vec{P}=mg\hat{\jmath}\). Por lo tanto, \[-k(l-l_0)\hat{\jmath}+mg\hat{\jmath}=0\] de donde: \[k=\frac{mg}{l-l_0}=\frac{0.08\mbox{ kg}\cdot 9.8\mbox{m/s}^2}{0.33\mbox{ m}-0.25\mbox{ m}}=\boxed{9.8\mbox{ N/m}}\]
El objeto realizará oscilaciones en torno a la posición de equilibrio. Si llamamos \(y\) la distancia desde esta posición, tal y como se muestra en la figura anterior, entonces: \[y(t)=A\sin\left(\omega t+\varphi_0\right)\] siendo \[\omega=\sqrt{\frac{k}{m}}=\sqrt{\frac{9.8\mbox{ N/m}}{0.08\mbox{ kg}}}=11.1\mbox{ rad/s}\] Para conocer \(A\) y \(\varphi_0\) tenemos que tener en cuenta, al igual que en los ejercicios anteriores, las condiciones en el instante inicial. Como \(y(0)=0.33 \text{ m}\) y \(v(0)=0\). Con esto tendremos: \[A=y(0)=0.33\mbox{ m}\] \[\varphi_0=\pi/2\mbox{ rad}\] Por lo cual: \[\boxed{y(t)=0.33\sin\left(11.1 t+\pi/2\right)\mbox{ m}}\] Fíjese que en efecto, \(y(t=0)=0.33\sin\left(\pi/2\right)\mbox{ m}=0.33\) m.
Para la velocidad: \[v(t)=\frac{dy}{dt}=\omega A\cos\left(\omega t+\varphi_0\right)\] Y sustituyendo: \[\boxed{v(t)=3.66\cos\left(11.1 t+\pi/2\right)\mbox{ m/s}}\] Fíjese que en efecto, \(v(t=0)=0.33\cos\left(\pi/2\right)\mbox{ m}=0\).
Dado que el valor máximo tanto del seno como del coseno es 1, los valores máximos de la posición y la velocidad serán: \[\boxed{x_{max}=A=0.33\mbox{ m}}\] \[\boxed{v_{max}=\omega A=3.66\mbox{ m/s}}\]
El péndulo de la figura tiene una longitud de 3 m. Inicialmente se separa de la vertical un ángulo \(3^\circ\) y se suelta. Calcular:
El periodo de las oscilaciones.
El máximo desplazamiento desde la vertical.
El tiempo que tarda en pasar por la vertical.
La posición en el instante \(t=2 \text{ s}\).
La dirección del movimiento en ese mismo instante.
SOLUCIÓN:
Dadas las características, como el ángulo es pequeño, el péndulo realiza un M.A.S. con frecuencia: \[\omega=\sqrt{\frac{g}{L}}\] Y por lo tanto, el periodo: \[T=2\pi\frac{1}{\omega}=2\pi\sqrt{\frac{L}{g}}\] Sustituyendo los valores del problema: \[T=2\pi\sqrt{\frac{3\mbox{ m}}{9.8\mbox{ m/s}^2}}=\boxed{3.48\mbox{ s}}\]
Dado que la energía cinética inicial es nula, la energía mecánica es únicamente energía potencial, es decir, en esta posición, la energía potencial es máxima. Por tanto, el desplazamiento es también máximo. En la siguiente figura se muestra un esquema de la posición inicial.
La coordenada \(x_{max}\) será: \[x_{max}=L\sin\alpha=L\sin 3^\circ=\boxed{0.157\mbox{ m}}\]
Dado que parte de la máxima distancia, el paso por la vertical es \(1/4\) de ciclo, por tanto tardará \(T/4\): \[t=\frac{T}{4}=\frac{3.48}{4}=\boxed{0.869\mbox{ s}}\]
Para calcularlo utilicemos: \[x(t)=A\sin\left(\omega t+\varphi_0\right)\] Dadas las condiciones del problema, como parte del reposo: \[v(0)=\omega A\cos\left(\omega\cdot 0+\varphi_0\right)=0\] Por lo que \(\varphi=\pi/2\). La posición en el instante inicial queda: \[x(0)=L\sin\alpha=A\sin\pi/2=A\] Por lo que: \[A=x(0)=0.157\mbox{ m}\] Y la frecuencia angular de las oscilaciones: \[\omega=\sqrt{\frac{g}{L}}=\sqrt{\frac{9.8\mbox{ m/s}^2}{3\mbox{ m}}}=1.81\mbox{ rad/s}\] Así, la posición en cualquier instante la podemos calcular con la función: \[x(t)=0.157\sin\left(1.81 t+\pi/2\right)\mbox{ m}\] En particular, la posición a los 2 s: \[x(t-2\mbox{ s})=0.157\sin\left(1.81\cdot 2+\pi/2\right)\mbox{ m}=\boxed{-0.139\mbox{ m}}\] Es decir, a la izquierda de la vertical, como se muestra en la figura:
La velocidad será: \[v(t)=\omega A \cos\left(\omega t+\varphi_0\right)=0.284\cos\left(1.81 t+\pi/2\right)\mbox{ m/s}\] Y sustituyendo \(t=2 \text{ s}\), \[v(t)=0.284\cos\left(1.81\cdot 2+\pi/2\right)\mbox{ m/s}=\boxed{0.131\mbox{ m/s}}\] Es decir, se mueve en la dirección positiva del eje x.
Se separa un péndulo 3\(^\circ\) de la vertical y se observa que el periodo de las oscilaciones es \(T=2.5 \text{ s}\). Si ahora se separa el péndulo 6\(^\circ\), ¿cuál será el periodo de estas oscilaciones?
SOLUCIÓN:
Dado que en ambos casos la desviación de la vertical es pequeña, el periodo vendrá dado por \(T=2\pi\sqrt{\frac{L}{g}}\), independiente de la amplitud de las oscilaciones. Por tanto, el periodo será el mismo: \(T=2.5 \text{ s}\).
Volver a la página principal de Física