Los estudiantes de geología tienen que estar capacitados para leer e interpretar los mapas topográficos con rapidez y exactitud, traduciendo las formas características que se ve en los mapas a expresiones verbales que abarquen clasificaciones, descripciones y aspectos evolutivos.
La información que se expone a continuación pretende enseñar a identificar los componentes del espacio geográfico y reconocer los conceptos propios de su estudio. También, representar e interpretar el espacio por medio de mapas para valorar la utilidad de la información geográfica en el mundo.
8.2 POSICION EN LA ESFERA TERRESTRE - LONGITUD Y LATITUD
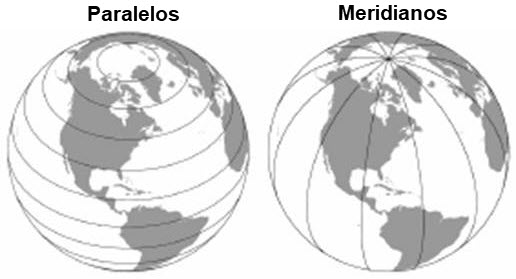
Si consideramos la tierra como una esfera, la mejor forma de establecer una posición en su superficie será mediante ángulos, es decir, mediante coordenadas angulares. Para establecer posiciones en la superficie terrestre utilizaremos una red geográfica compuesta por una serie de líneas denominadas:
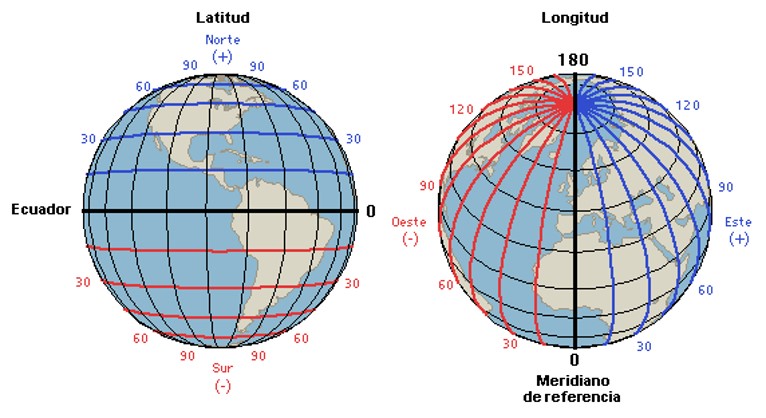
La localización de cualquier punto en la superficie terrestre vendrá dado por su longitud y su latitud:
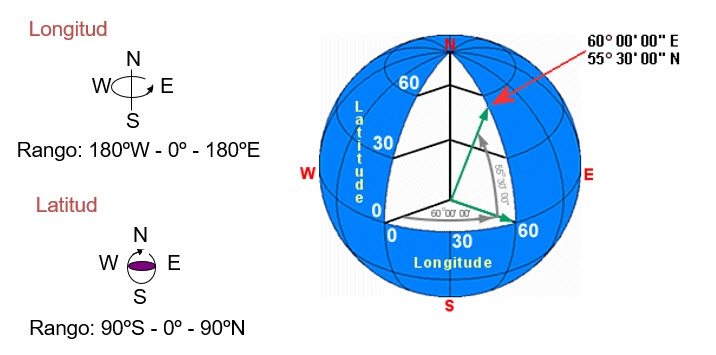
Longitud: arco de paralelo, medido en grados, entre el lugar considerado y el meridiano principal (Greenwich: 0º). Se mide hacia el E o el W por el camino más corto. Oscila entre 0º y 180º
Latitud: arco de meridiano (medido en grados) entre el lugar considerado y el ecuador (paralelo 0º). Se mide hacia el N o hacia el S. Oscila entre 0º y 90º (en los polos).
8.3 ESFERA, ESFEROIDE, GEOIDE Y DATUM
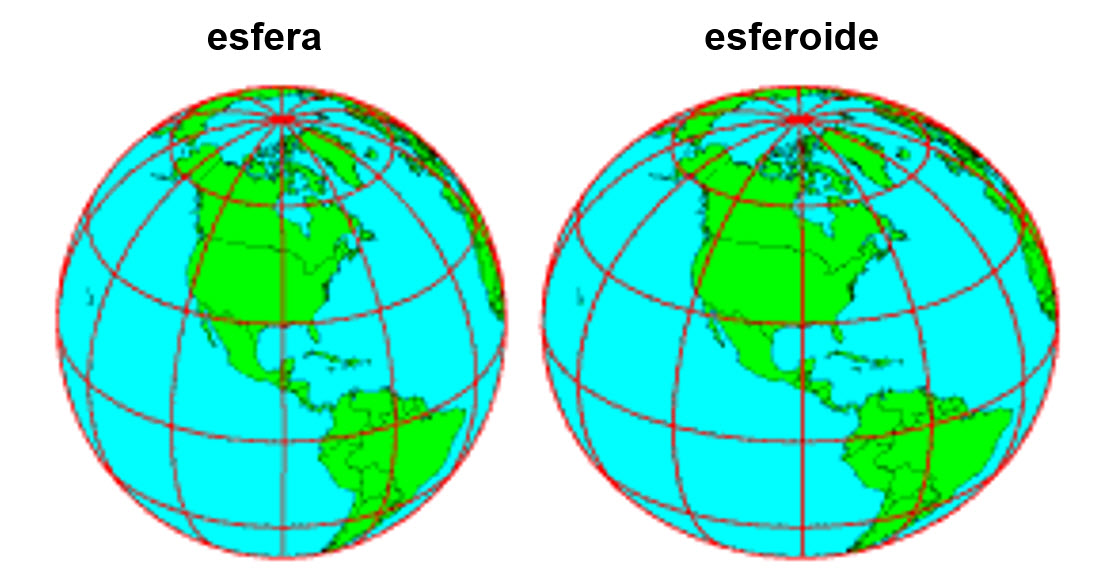
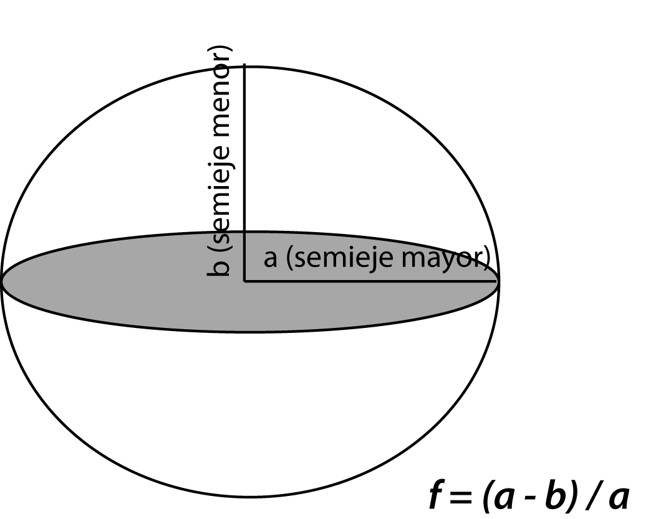
Representar la tierra mediante una esfera no es lo más exacto, puesto que está ligeramente achatada por los polos. Un elipsoide (figura geométrica tridimensional formada por la revolución de una elipse) es más exacto para representar la superficie terrestre. Mientras que para definir una esfera solamente necesitaremos su radio, para definir un elipsoide necesitaremos sus dos semiejes; semieje mayor y semieje menor. En el caso de la Tierra, ambos semiejes serán bastante parecidos (su variación es menor de un 0.5 %), con lo que a este elipsoide se le suele denominar también esferoide (elipsoide muy próximo a una esfera).
Para definir un elipsoide podemos utilizar:
Sus dos semiejes; mayor (a) y menor (b)
El semieje mayor (a) y el achatamiento expresado como 1/f
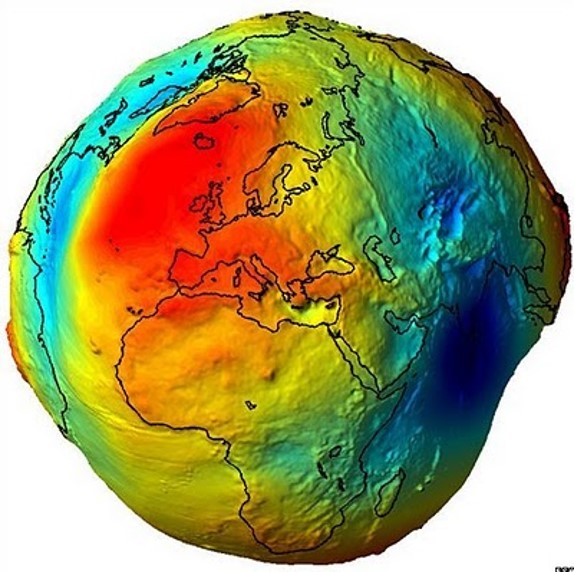
La superficie terrestre es irregular y bastante compleja, con montañas de hasta 8000 metros como el Himalaya y fosas de hasta 10000 metros como la fosa de las marianas. Parece obvio que ni esfera ni esferoide serán capaces de reflejar esta complejidad, pues son figuras geométricas relativamente simples. Sin embargo, tenemos otro tipo de superficie que es capaz de captar estas irregularidades; el geoide. El geoide se define como la superficie equipotencial de la gravedad medida a nivel del mar. El geoide representa la forma teórica de la tierra, y aunque no refleja las variaciones totales (las variaciones del geoide son de +/- 100m), sí que representa una superficie irregular que simula la forma terrestre.
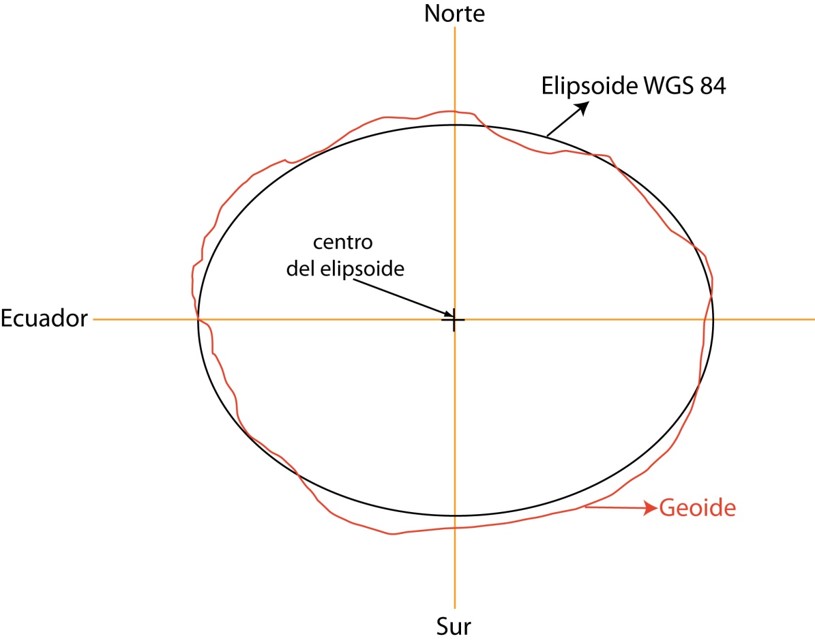
Aunque esta representación terrestre sería la que más se aproxima a la forma terrestre (el geoide es considerado la forma teórica de la tierra), al no ser una figura geométrica regular, no es apta para definir un sistema de coordenadas. Para definir la posición de un punto en la superficie terrestre siempre utilizaremos un esferoide, pero dado que la tierra es bastante irregular, tendremos que “alinear” este esferoide con la forma teórica terrestre (el geoide). La solución que la cartografía le da a este problema es la utilización de un Datum.
Un Datum estará formado por un esferoide, y los parámetros matemáticos para alinear este esferoide con el geoide (forma teórica terrestre). Debido a que la Tierra es irregular, no existe un solo datum, es decir, no tenemos una única forma de alinear esferoide con geoide, ni tampoco un único esferoide en uso. Existen dos tipos fundamentales de datums:
Datum geocéntrico o global: Utilizado para representaciones globales de la Tierra. Alinea el centro del esferoide con el centro de masas terrestre (centro del geoide). El más importante es el World Geodetic System de 1984, que utiliza un esferoide calculado mediante GPS. Este el datum que utilizan los sistemas de posicionamiento global como GPS, GLONASS o GALILEO , y también el más utilizado para los mapas globales que podemos encontrar en internet (Google Maps, Google Earth, Bings Maps, etc.).
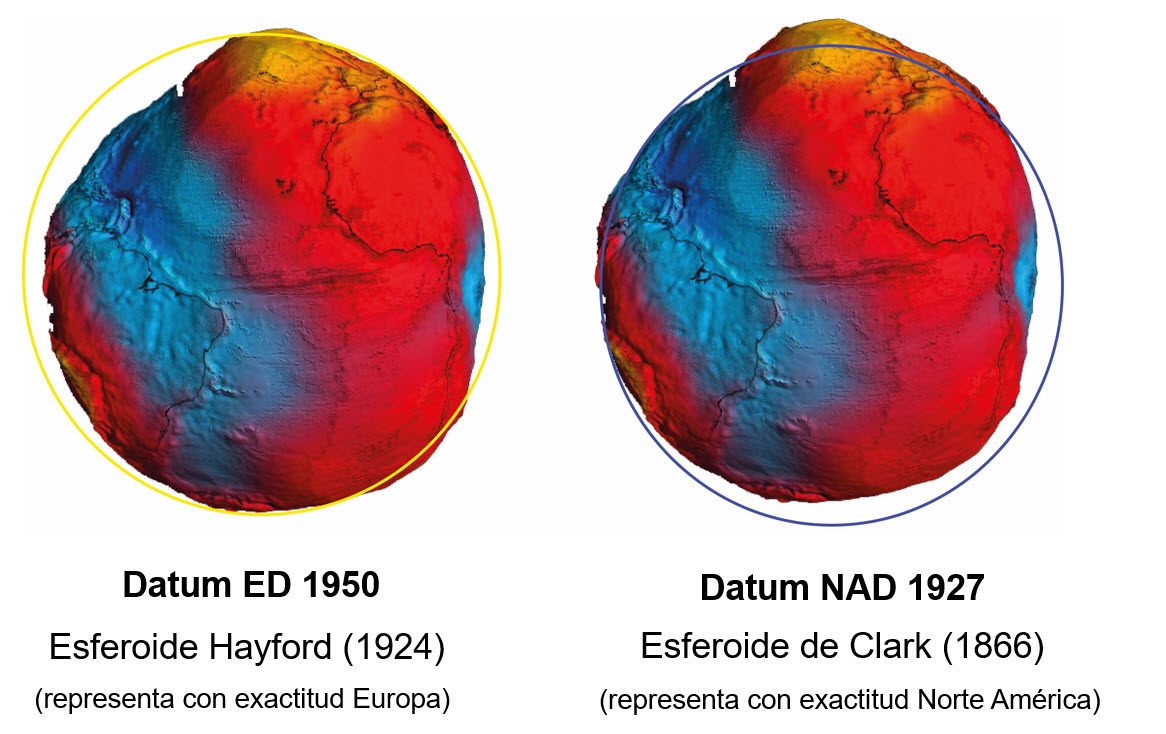
Datum local: Utilizado para representaciones locales o regionales. Un datum global alinea un esferoide con la parte de la superficie terrestre que queramos representar con mayor exactitud, haciendo que en esa región, esferoide y geoide sean tangentes. Existen multitud de datum locales.
8.4 SISTEMAS DE PROYECCIÓN
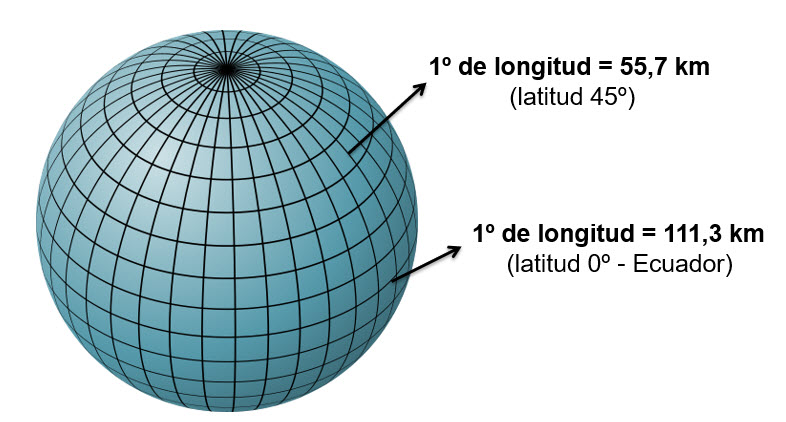
Como hemos visto, la manera más eficaz de representar la superficie terrestre es mediante un datum (combinación de un esferoide y sus parámetros de alineamiento con el geoide). Sin embargo, un datum, al utilizar un esferoide, utiliza coordenadas angulares (longitud y latitud). Esto no es lo más adecuado si queremos realizar medidas, pues mientras que un grado de longitud en el ecuador mide aproximadamente 111 km, a latitud 60º mide casi la mitad.
Si a esto le sumamos que todos los soportes que vamos a utilizar para representaciones cartográficas son planos (papel, pantalla de ordenador, etc.), se hace necesario representar está superficie esférica en un plano.
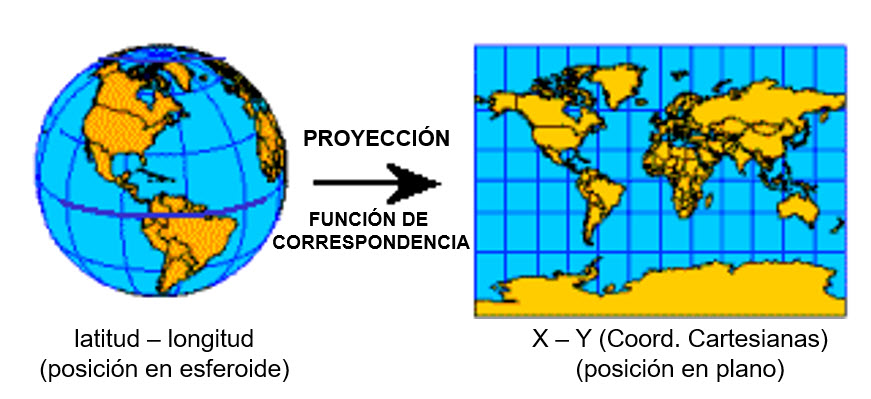
Un sistema de proyección se define como un conjunto de funciones de correspondencia, que transformarán una posición en el esferoide (latitud–longitud, sistema angular), en una posición en un plano (X-Y, sistema cartesiano).
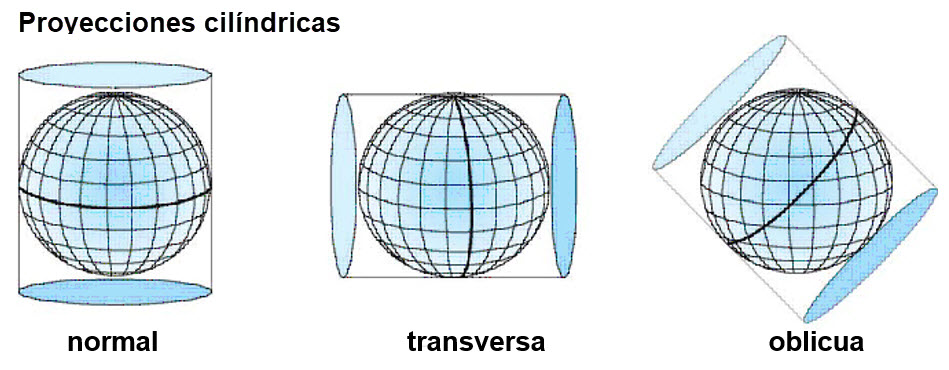
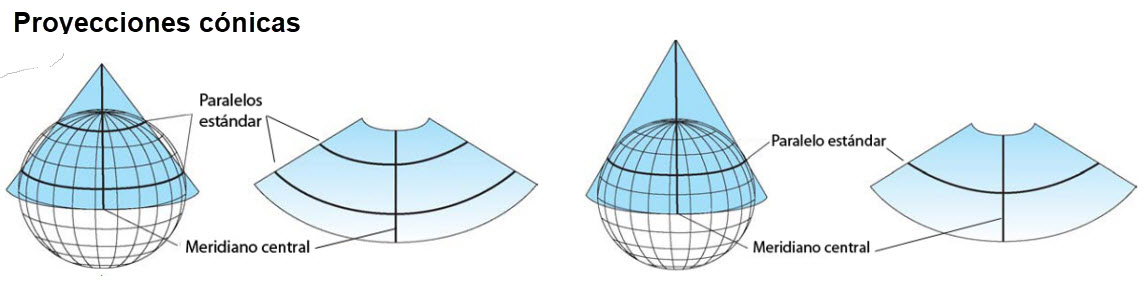
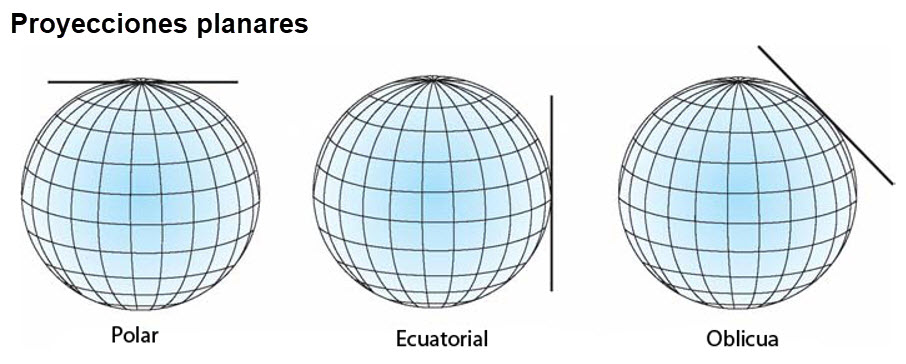
Para proyectar la superficie terrestre en un plano, se utilizan figuras geométricas “desarrollables”, es decir, figuras que se puedan transformar en un plano sin distorsión. Las principales figuras geométricas utilizadas para proyectar serán el cilindro, el cono y el plano. Al proyectar circunscribimos la superficie terrestre dentro de estas figuras:
Sin embargo, el proyectar la superficie terrestre en estas superficies no es sencillo, e implica un proceso en el que las propiedades geométricas se distorsionarán, principalmente área, forma y distancias. Es imposible mantener sin distorsionar a la vez estas tres propiedades geométricas, pero si que podemos mantener una de ellas distorsionando mucho las demás. Los tipos de proyecciones, según las propiedades geométricas que preserven serán:
Proyección conforme: Mantiene las formas (relaciones angulares)
Proyección equiareal o equivalente: Mantiene las proporciones (áreas)
Proyección equidistante: Mantiene las distancias desde el centro del mapa
Para definir un sistema de proyección, utilizaremos una figura desarrollable y las propiedades geométricas que se mantendrán o deformarán. Así pues, una proyección de Mercator es realmente una proyección cilíndrica normal conforme.