En Física, algunas cantidades como el tiempo, la temperatura, la masa y la densidad, se pueden describir completamente con un número y una unidad. Diremos entonces que se trata de magnitudes escalares.

Sin embargo, existen otras magnitudes que están asociadas con una dirección y no pueden describirse con un sólo número. Por ejemplo, la velocidad: no solo es necesario indicar la rapidez de un avión, sino también su dirección. También ocurre igual con la magnitud física fuerza: para describirla correctamente, hay que indicar no solo su intensidad, sino también su dirección y sentido. Diremos que son magnitudes vectoriales.

EJEMPLO: \({\overrightarrow{A}}\) y \({\overrightarrow{B}}\) son vectores con la misma magnitud y dirección, pero diferente sentido. El vector \({\overrightarrow{C}}\) tiene la misma dirección que los dos vectores anteriores. Diremos que son vectores paralelos.

La magnitud de un vector es el módulo del vector, y se expresa en la forma \(|{\overrightarrow{A}}|\). Es una cantidad escalar y siempre es positiva.

1. Suma de vectores:

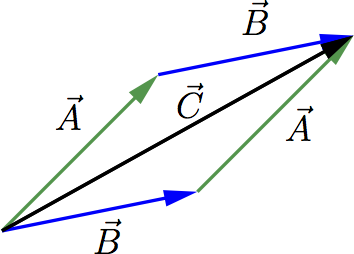
   Supongamos que una partícula sufre un desplazamiento del punto \(O\) al punto \(P\), definido por el vector \({\overrightarrow{A}}={\overrightarrow{OP}}\), seguido de un segundo desplazamiento, del punto \(P\) al punto \(Q\), definido entonces por el vector \({\overrightarrow{B}}={\overrightarrow{PQ}}\). El resultado final será equivalente a considerar que la partícula parte del punto \(O\) y tiene como punto final el punto \(Q\). Es decir, podemos considerar que el desplazamiento total vendrá dado por el vector \({\overrightarrow{C}}\), que se calcula como \[{\overrightarrow{C}} = {\overrightarrow{A }}+{\overrightarrow{B}} = {\overrightarrow{B}}+{\overrightarrow{A}}\]

   La suma de vectores es conmutativa, tal y como vemos en la siguiente figura

   

   Y además, también es asociativa:

   \[ {\overrightarrow{A}}+{\overrightarrow{B}}+{\overrightarrow{C}} \rightarrow \left ( {\overrightarrow{A}}+{\overrightarrow{B}} \right ) + {\overrightarrow{C}} = {\overrightarrow{A}} + \left ( {\overrightarrow{B}} + {\overrightarrow{C}} \right )\]

   Para restar dos vectores:

   \[{\overrightarrow{A}} - {\overrightarrow{B}} = {\overrightarrow{A}} + \left ( -{\overrightarrow{B}} \right )\]

   \((-{\overrightarrow{B}})\) es el vector opuesto de \({\overrightarrow{B}}\). Tiene la misma magnitud, la misma dirección, pero sentido contrario.

   También podemos multiplicar un vector por un escalar. Por ejemplo:

   \[{\overrightarrow{B}} = 2 \, {\overrightarrow{A}}\]

   \({\overrightarrow{B}}\) es un vector con la misma dirección y sentido que \({\overrightarrow{A}}\) pero su magnitud es el doble.

   La fuerza es una magnitud vectorial. Por tanto, de la expresión

   \[ {\overrightarrow{F}}= m \, {\overrightarrow{a}} \,\]

   podemos deducir que la dirección de \({\overrightarrow{F}}\) y \({\overrightarrow{a}}\) es la misma, el sentido también (porque \(m\) es siempre una cantidad positiva) y la magnitud de \({\overrightarrow{F}}\) es igual a la magnitud de \({\overrightarrow{a}}\) multiplicada por la masa \(m\).

   EJEMPLO: Un senderista camina desde un refugio en una llanura \(1\) km hacia el norte y \(2\) km hacia el este. ¿A qué distancia y en qué dirección está respecto al punto de partida? Solución

   Solución:

   El camino que sigue el senderista puede ser descrito mediante los vectores \({\overrightarrow{A}}\), \({\overrightarrow{B}}\) y su resultante \({\overrightarrow{C}}\), tal y como se representa en la siguiente figura

   

   La distancia al punto de partida la determinaremos mediante la magnitud del vector \({\overrightarrow{C}}\), que vendrá dada por:

   \[|{\overrightarrow{C}}| = \sqrt{1 + 4} \; {\rm km} = \sqrt{5} \; {\rm km} \, .\]

   La dirección nos la dará el ángulo \(\phi\) y por tanto, puede ser calculado teniendo en cuenta la magnitud de los vectores \({\overrightarrow{A}}\) y \({\overrightarrow{B}}\), \(1\) y \(2\) km, respectivamente. Por tanto

   \[{\rm tg} \, \phi = \frac{2}{1} \;\; \rightarrow \phi=63.4^{\rm o}\]




2. Componentes

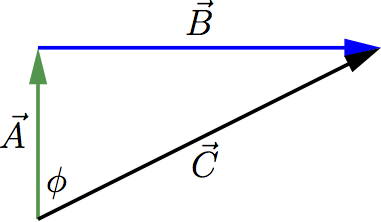
   Las componentes de los vectores nos van a permitir un método sencillo pero general para sumar vectores. Supongamos que tenemos un sistema cartesiano de ejes de coordenadas. Entonces \(A_x\) es la magnitud del vector \({\overrightarrow{A_x}}\) y \(A_y\) es la magnitud del vector \({\overrightarrow{A_y}}\). \(A_x\) y \(A_y\) son las componentes del vector \({\overrightarrow{A}}\). Podemos calcular las componentes del vector \({\overrightarrow{A}}\) si conocemos la magnitud y la dirección de dicho vector. Describiremos la dirección de un vector con su ángulo \(\theta\), relativo a una dirección de referencia, que es el eje \(x\) positivo, siempre en sentido antihorario

   \[\frac{A_x}{|{\overrightarrow{A}}|} = \cos \theta \rightarrow A_x= |{\overrightarrow{A}}| \cos \theta \quad \quad \frac{A_y}{|{\overrightarrow{A}}|}= {\rm sen}\, \theta \rightarrow A_y= |{\overrightarrow{A}}| {\rm sen} \, \theta\]

   EJEMPLO: Determina las componente \(x\) e \(y\) del vector \({\overrightarrow{D}}\), con magnitud \(|{\overrightarrow{D}}|=3\) m y siendo \(\alpha=45^{\rm o}\) (ver figura). Solución

   Solución:

   Según la figura, vemos que \(D_x\) es positiva y \(D_y\) es negativa. Por tanto

   \[\cos \alpha = \frac{D_x}{|{\overrightarrow{D}}|} \quad {\rm sen} \, \alpha = \frac{|D_y|}{|{\overrightarrow{D}}|} \rightarrow D_x=3/2 \sqrt{2} \quad D_y=3/2 \sqrt{2} \, .\]

   
   

3. Cálculo de vectores usando componentes

   El uso de componentes facilita algunos cálculos que implican vectores. Veamos algunos ejemplos

   • Cálculo y magnitud de un vector a partir de sus componentes:

     Un vector queda descrito por su magnitud y dirección, pero también dando sus componentes. A partir de ellas, podemos calcular la magnitud y dirección del vector

     \[ |{\overrightarrow{A}}| = \sqrt{A_x^2 + A_y^2} \quad {\rm tg} \, \theta = \frac{A_y}{A_x} \quad \theta = {\rm arctg} \, \, \frac{A_y}{A_x}\]

     EJEMPLO: Calcula la magnitud y dirección del vector \({\overrightarrow{A}}\) si \(A_x=2\) m y \(A_y=-2\) m. Solución

     Solución:

     \[ |{\overrightarrow{A}}| = \sqrt{A_x^2 + A_y^2} =\sqrt{8} \quad \theta = {\rm arctg} \, \,(-1) \quad \theta=315^{\rm o}\]

     Al introducir el valor \(-1\) en la calculadora para obtener el valor del arco tangente, nos dará \(-45^{\rm o}\). Este ángulo, siguiendo nuestro criterio de tomarlo respecto al eje \(x\) positivo, en sentido antihorario, es equivalente al ángulo de \(315^{\rm o}\).

   
   

   • Multiplicación de un vector por un escalar:

     \[ {\overrightarrow{D}}= c {\overrightarrow{A}} \rightarrow D_x = c \, A_x \quad D_y = c \, A_y\]

   • Uso de componentes para calcular la suma de vectores:

     \[ {\overrightarrow{A}}, {\overrightarrow{B}} \quad {\overrightarrow{R}} = {\overrightarrow{A}} + {\overrightarrow{B}} \rightarrow R_x=A_x+B_x \quad R_y=A_y+B_y \, .\]

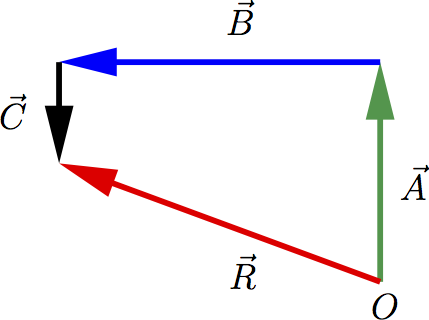
   EJEMPLO: Un conductor desorientado recorre \(3.25\) km hacia el norte, \(4.75\) km hacia el oeste y \(1.50\) km hacia el sur. Calcular la magnitud y dirección del vector desplazamiento resultante, mediante la suma de las componentes.

   

   Solución

   Solución:

   Teniendo en cuenta las componentes (expresadas en km):

   \[ A_x=0 \;\; A_y=3.25 \quad B_x=-4.75 \, \, B_y= 0 \quad C_x= 0 \;\; C_y=-1.50\]

   Por tanto

   \[ R_x=A_x+B_x+C_x=-4.75 \quad R_y=A_y+B_y+C_y=1.75 \, .\]

EJEMPLO: El vector \({\overrightarrow{A}}\) tiene componentes \(A_x=1.30\) cm. \(A_y=2.25\) cm. El vector \({\overrightarrow{B}}\) tiene componentes \(B_x=4.10\) cm y \(B_y=-3.75\) cm. Calcular:

1. Las componentes de la resultante \({\overrightarrow{R}}={\overrightarrow{A}}+{\overrightarrow{B}}\).

2. La magnitud y la dirección de \({\overrightarrow{R}}={\overrightarrow{A}}+{\overrightarrow{B}}\).

3. Las componentes de la diferencia vectorial \({\overrightarrow{S}}={\overrightarrow{B}}-{\overrightarrow{A}}\).

4. La magnitud y la dirección de \({\overrightarrow{S}}={\overrightarrow{B}}-{\overrightarrow{A}}\).

Solución

Solución:

1. \[ R_x=A_x+B_x=5.40 \; {\rm cm} \quad \quad R_y=A_y+B_y=-1.50 \; {\rm cm}\]

2. \[|{\overrightarrow{R}}|=\sqrt{(5.40)^2 + (1.50)^2} \; {\rm cm} = 5.60 \; {\rm cm} \quad \quad {\rm tg} \; \phi= \frac{-1.50}{5.40} \rightarrow \phi=285.52^{\rm o}\]

3. \[S_x=B_x-A_x=2.80 \; {\rm cm} \quad \quad S_y=B_y-A_y=-6.00 \; {\rm cm}\]

4. \[|{\overrightarrow{S}}|=\sqrt{(2.80)^2 + (6.00)^2} \; {\rm cm} = 6.62 \; {\rm cm} \quad \quad {\rm tg} \; \psi= \frac{-6.00}{2.80} \rightarrow \psi=115.02^{\rm o}\]

Los vectores unitarios son aquéllos con magnitud igual a \(1\) (sin unidades). Su única finalidad es dar una dirección en el espacio. Siempre los notaremos con un acento del tipo \(\hat{ }\), para indicar que se trata de un vector unitario.

• \(\hat{\imath}\) \(\rightarrow\) apunta en la dirección \(x\) positiva.

• \(\hat{\jmath}\) \(\rightarrow\) apunta en la dirección \(y\) positiva

Por tanto, podemos escribir:

\[{\overrightarrow{A}}= A_x \, \hat{\imath} \, + \, A_y \, \hat{\jmath} \, .\]

Y la suma de vectores se haría sumando directamente componentes: \[\vec{A}=A_x \, \hat{\imath} \, + \, A_y \, \hat{\jmath} \quad \quad \quad \vec{B}=B_x \, \hat{\imath} \, + \, B_y \, \hat{\jmath} \quad \quad \quad {\overrightarrow{R}}= {\overrightarrow{A}}+{\overrightarrow{B}}=\left ( A_x+B_x \right) \hat{\imath} + \left (A_y+B_y \right) \hat{\jmath}\]

1. Producto escalar de dos vectores:
   

   Se denota por \({\overrightarrow{A}} \cdot {\overrightarrow{B}}\) y el resultado es un escalar. Para calcularlo, representamos los vectores \({\overrightarrow{A}}\) y \({\overrightarrow{B}}\) con origen en el mismo punto.

   

   Definimos \({\overrightarrow{A}} \cdot {\overrightarrow{B}}\) como la magnitud de \({\overrightarrow{A}}\) multiplicada por la componente de \({\overrightarrow{B}}\) paralela a \({\overrightarrow{A}}\), es decir:

   \[\fbox{${\overrightarrow{A}} \cdot {\overrightarrow{B}} = |{\overrightarrow{A}}|\, |{\overrightarrow{B}}| \, {\rm cos} \, \theta$ }\]

   Es un escalar, y puede ser positivo, negativo o cero. Si \(\theta= \pi /2\) (vectores perpendiculares) el producto escalar es siempre cero, independientemente de la magnitud de los vectores. También podemos comprobar que el producto escalar es conmutativo:

   \[{\overrightarrow{A}} \cdot {\overrightarrow{B}} = |{\overrightarrow{A}}| \, |{\overrightarrow{B}}| \, {\rm cos} \, \theta= |{\overrightarrow{B}}| \, |{\overrightarrow{A}}| \, {\rm cos} \, \theta = {\overrightarrow{B}} \cdot {\overrightarrow{A}}\]

   Por ejemplo, si una fuerza constante \(\vec{F}\) se aplica a un cuerpo que sufre un desplazamiento \(\vec{s}\), el trabajo \(W\) realizado por la fuerza se calculará como

   \[\fbox{$W = {\overrightarrow{F}} \cdot {\overrightarrow{s}} $ }\]

   Si queremos usar las componentes para calcular el producto escalar de los vectores \({\overrightarrow{A}}\) y \({\overrightarrow{B}}\)

   \[{\overrightarrow{A}}= A_x \hat{\imath} + A_y \hat{\jmath} \quad \; {\overrightarrow{B}}= B_x \hat{\imath} + B_y \hat{\jmath} \,\]

   tendremos: \[\vec{A} \cdot \vec{B} = \left ( A_x \hat{\imath} + A_y \hat{\jmath} \right ) \cdot \left ( B_x \hat{\imath} + B_y \hat{\jmath} \right ) = A_x \, B_x + A_y \, B_y \, ,\] donde hemos usado que se verifica que: \[\hat{\imath} \cdot \hat{\imath} = \hat{\jmath} \cdot \hat{\jmath}= 1 \quad \; \hat{\imath} \cdot \hat{\jmath} = \hat{\jmath} \cdot \hat{\imath} = 0\]

   EJEMPLO: Obtener el producto escalar de los vectores \({\overrightarrow{A}}\) y \({\overrightarrow{B}}\), siendo \(|{\overrightarrow{A}}|=4\), \(\theta_A=53^{\rm o}\) y \(|{\overrightarrow{B}}|=5\), \(\theta_B=130^{\rm o}\) ¹

   

   Solución

   Solución:

   Podemos calcular las componentes de cada uno de los vectores: \[A_x= |{\overrightarrow{A}}| \cos 53^{\rm o} = 2.407 \quad \; A_y = |{\overrightarrow{A}}| {\rm sen} 53^{\rm o}=3.195\]

   \[B_x= |{\overrightarrow{B}}| \cos 130^{\rm o} = -3.214 \quad \; B_y = |{\overrightarrow{B}}| {\rm sen} 130^{\rm o}=3.830 \, .\]

   Por tanto:

   \[ {\overrightarrow{A}} \cdot {\overrightarrow{B}} = A_x \, B_x \, + \, A_y \, B_y = 4.499 \, .\]

EJEMPLO: Determinar el ángulo de los vectores \({\overrightarrow{A}} = 2 \hat{\imath} + 3 \hat{\jmath}\) y \({\overrightarrow{B}} = -4 \hat{\imath} + 2 \hat{\jmath} \, .\) Solución

Solución:

Usando la definición de producto escalar:

\[ {\overrightarrow{A}} \cdot {\overrightarrow{B}} = -8 + 6 = -2 = |{\overrightarrow{A}}| \, |{\overrightarrow{B}}| \, \cos{\theta}\]

Pero: \[|{\overrightarrow{A}}| = \sqrt{4 +9}=\sqrt{13} \quad \; |{\overrightarrow{B}}|= \sqrt{16+4}= \sqrt{20} \, .\]

Por tanto: \[ -2 = |{\overrightarrow{A}}| \, |{\overrightarrow{B}}| \, \cos{\theta} = \sqrt{13} \, \sqrt{20} \cos{\theta} \; \rightarrow \; \theta = {\rm arc \, cos} \left (\frac{-2}{\sqrt{260}} \right ) = 97.125^{\rm o}\]




2. Producto vectorial de dos vectores:
   

   El producto vectorial de los vectores \({\overrightarrow{A}}\) y \({\overrightarrow{B}}\) se denota como \({\overrightarrow{A}} \wedge {\overrightarrow{B}}\). Definimos dicho producto vectorial como un vector, perpendicular al plano que forman los vectores \({\overrightarrow{A}}\) y \(\vec{B}\), y cuya magnitud viene dada por \[|{\overrightarrow{A}} \wedge {\overrightarrow{B}}| = |{\overrightarrow{A}}| \, |{\overrightarrow{B}}| \, {\rm sen} \theta \, ,\] siendo \(\theta\) el ángulo que forman ambos vectores. La dirección y sentido del vector \({\overrightarrow{A}} \wedge {\overrightarrow{B}}\) nos lo da la regla de la mano derecha. La dirección del producto vectorial está definida por la dirección del pulgar, cerrando los demás dedos en torno al vector \({\overrightarrow{A}}\) primero y siguiendo con el vector \({\overrightarrow{B}}\).

   Una propiedad del producto vectorial es que cuando ambos vectores son paralelos (\(\theta=0\), \(180^{\rm o}\)), el producto vectorial es nulo.

   Teniendo en cuenta los vectores unitarios en el espacio tridimensional:

   

   Podemos ver que verifican: \[\hat{\imath} \wedge \hat{\jmath} = \hat{k} \quad \; \hat{\jmath} \wedge \hat{\imath} = -\hat{k} \quad \; \hat{\imath} \wedge \hat{\imath} = 0\]

   \[\hat{\jmath} \wedge \hat{k} = \hat{\imath} \quad \; \hat{k} \wedge \hat{\jmath} = -\hat{\imath} \quad \; \hat{\jmath} \wedge \hat{\jmath} = 0\]

   \[\hat{k} \wedge \hat{\imath} = \hat{\jmath} \quad \; \hat{\imath} \wedge \hat{k} = -\hat{\jmath} \quad \; \hat{k} \wedge \hat{k} = 0\]

   Y esto nos sirve para escribir una expresión general para el producto vectorial \({\overrightarrow{A}} \wedge {\overrightarrow{B}}\):

   \[{\overrightarrow{A}} \wedge {\overrightarrow{B}} = \left ( A_x \hat{\imath} + A_y \hat{\jmath} + A_z \hat{k} \right ) \wedge \left (B_x \hat{\imath} + B_y \hat{\jmath} + B_z \hat{k} \right ) = \left ( A_y\, B_z\, -\, A_z\, B_y \right)\hat{\imath} + \left ( A_z\, B_x\, -\, A_x\, B_z \right)\hat{\jmath} + \left ( A_x\, B_y\, -\, A_y\, B_x \right)\hat{k} \,\]

   que puede escribirse en forma más sencilla como un determinante:

   \[ {\overrightarrow{A}} \wedge {\overrightarrow{B}} = \left | \begin{matrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ A_x & A_y & A_z \\ B_x & B_y & B_z \end{matrix} \right |\]

   EJEMPLO: Sea \({\overrightarrow{A}}= 6 \, \hat{\imath}\) y \({\overrightarrow{B}}= 4 \left ( \cos 30^{\rm o} \, \hat{\imath} + {\rm sen} \, 30^{\rm o} \, \hat{\jmath} \right )\). Calcula \({\overrightarrow{A}} \wedge {\overrightarrow{B}}\). Solución

   Solución:

   \[{\overrightarrow{A}} \wedge {\overrightarrow{B}} = 24 \cdot {\rm sen} \, 30^{\rm o} \, \hat{k} = 12 \, \hat{k}\]